Опыт Юнга. Расчет интерференционной картины от двухисточников. Расстояние между полосами.

Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S₁ и S₂ (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S₁ и S₂, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

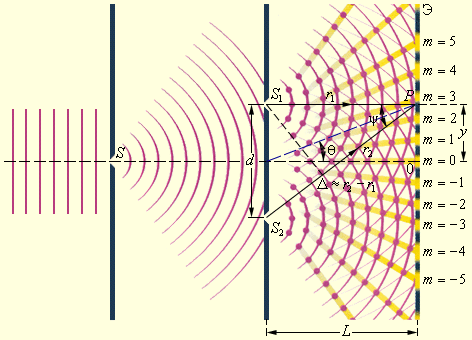Рисунок 3.7.3. Схема интерференционного опыта Юнга

Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S₁ и S₂, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S₁ и S₂, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r₁и r₂. Следовательно, фазы колебаний, создаваемых волнами от источников S₁ и S₂ в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S₁ и S₂распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.

Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора 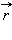, записывается в виде 

где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ: 

Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A².

Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P: 

(*)

где Δ = r₂ – r₁ – так называемая разность хода.

Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом I_max = (a₁ + a₂)² > I₁ + I₂. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивностиI_min = (a₁ – a₂)² < I₁ + I₂. На рис. 3.7.4 показано распределение интенсивности света в интерференционной картине в зависимости от разности хода Δ.

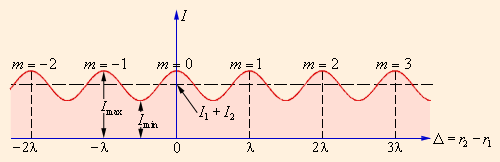Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума

В частности, если I₁ = I₂ = I₀, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид: 

В этом случае I_max = 4I₀, I_min = 0.

Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.

Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить: 

При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно, 

где ψ – угол схождения «лучей» в точке наблюдения P. Выполним количественную оценку. Допустим, что расстояние d между щелями S₁ и S₂ равно 1 мм, а расстояние от щелей до экрана Э составляет L = 1 м, тогда ψ = d / L = 0,001 рад. Для зеленого света (λ = 500 нм) получим Δl = λ / ψ = 5 · 10⁵ нм = 0,5 мм. Для красного света (λ = 600 нм) Δl = 0,6 мм. Таким путем Юнг впервые измерил длины световых волн, хотя точность этих измерений была невелика.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.