Магнитное поле. Взаимодействие токов. Закон АмпераЭкспериментальные факты. 1. Постоянные магниты. В природе существуют вещества с особыми свойствами, из которых можно сделать постоянные магниты. Установлены следующие факты: У каждого постоянного магнита есть две области, вблизи которых особые свойства магнитов проявляются особенно сильно. Эти области носят название северного (N) и южного (S) полюсов магнита, так как магнитная стрелка, сделанная из соответствующего вещества, указывает своим северным полюсом на север и южным полюсом на юг Земли. Два полюса магнита аналогичны двум типам электрических зарядов. Одинаковые магнитные полюса отталкиваются, а разноименные полюса притягиваются. Невозможно изолировать северный или южный полюс магнита. Всякая попытка разделить магнит кончается тем, что возникают два меньших магнита, имеющих оба полюса. Магниты оказывают силовое воздействие на некоторые природные вещества, содержащие железо, никель или кобальт. 2. Взаимодействие токов. Если в цепь постоянного тока включить два провода, то: Последовательно включенные параллельные близко расположенные проводники отталкиваются . Параллельно включенные проводники притягиваются . 3. Механическое воздействие тока. Магнитная стрелка отклоняется вблизи проводника, по которому течет ток. Рамка с током поворачивается, если по проводнику пропускается ток. Магнитное поле. Все указанные экспериментальные факты свидетельствуют о том, что в пространстве, окружающем постоянный магнит или провод с током, возникает магнитное поле , оказывающее силовое воздействие на пробные тела (постоянные магниты или проводники с током). По аналогии с напряженностью электрического поля E можно ввести понятие вектора магнитной индукции В . В каждой точке пространства можно установить направление вектора В , считая по определению, что оно совпадает с направлением от южного к северному полюсу свободно подвешенной в этой точке пространства магнитной стрелки . Сплошные линии, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции В , называютсясиловыми линиями магнитного поля . Как показывают простые опыты, силовые линии магнитного поля всегда замкнуты. Этим магнитное поле принципиально отличается от электрического поля, силовые линии которого всегда начинаются и оканчиваются на зарядах. Замкнутость силовых линий магнитного поля есть следствие отсутствия в природе изолированных магнитных полюсов. Векторные поля, силовые линии которых замкнуты, называются вихревыми полями . Магнитное поле - вихревое. Магнитные поля от разных источников в данной точке пространства складываются по правилу сложения векторов (принцип суперпозиции) Закон Ампера. Пусть проводник с током внесен в область магнитного поля. На этот проводник действует сила, направление и величина которой определяется законом Ампера: (см. ниже) Удобно использовать для определения направления силы Ампера правило левой руки. Из формулы закона Ампера следует, что сила Ампера достигает максимального значения Fмакс при q=p/2 , т.е. когда проводник расположен перпендикулярно вектору магнитной индукции. Величина вектора магнитной индукции B определяется как отношение F макс /Idl ; иными словами, (см. ниже) Единица магнитной индукции определяется из этой формулы и равна магнитной индукции такого однородного поля, в котором на участок проводника длиной 1 м действует сила 1 Н при силе тока в проводнике 1 А: [B] = Н/(А·м) = Тл (тесла). Сила  , с которой магнитное поле действует на элемент объёма dV проводника с током плотности  , находящегося в магнитном поле с индукцией  :  .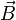
Если ток течёт по тонкому проводнику, то  , где  — «элемент длины» проводника — вектор, по модулю равный dl и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.
Модуль силы Ампера можно найти по формуле:  ,
где α — угол между векторами магнитной индукции и тока. Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ( ):  .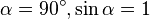
|