Главная » Самолетостроение » Физика » Энергетические соотношения колебательного процесса

Энергетические соотношения колебательного процесса

Соотношения Мэнли — Роу

Материал из Википедии — свободной энциклопедии

Соотношения Мэнли — Роу — энергетические соотношения, характеризующие взаимодействие колебаний или волн в нелинейных системах с сосредоточенными или распределёнными параметрами. Они были впервые получены в 1956 году Дж. Мэнли и Г. Э. Роу для колебаний в нелинейной реактивной системе с сосредоточенными параметрами, а впоследствии обобщены на волны в нелинейных средах.

Соотношения Мэнли — Роу справедливы для системы с произвольной реактивной нелинейностью. В совокупности с законами сохранения энергии и импульса, соотношения Мэнли — Роу определяют характер нелинейного взаимодействия волн (колебаний) и позволяют рассчитать максимальную эффективность преобразователя частоты на реактивной нелинейности.

Общий вид

В общем виде соотношения Мэнли — Роу могут быть записаны следующим образом:

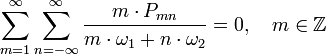
$\sum_{m=1}^\infty\sum_{n=-\infty}^\infty\frac{m\cdot$

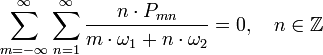
$\sum_{m=-\infty}^\infty\sum_{n=1}^\infty\frac{n\cdot$

где

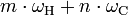$P m n$ — изменение мощности на комбинационной частоте $m\cdot\omega_\text{H}+n\cdot\omega_\text{C}$ ,
$ω 1,ω 2$ — частоты исходных колебаний (волн). Причём отношение $\frac{\omega_2}{\omega_1}$ должно быть иррационально, поскольку в противном случае, возможно выразить все частоты как гармоники одной фундаментальной частоты.

Первое из соотношений Мэнли — Роу представляет собой закон сохранения числа квантов, которые в зависимости от природы взаимодействующих волн представляют собой фотоны, фононы, плазмоны, магноны или другие взаимодействующие квазичастицы.

Можно вычислить следующие величины:

$A_{mn}=\frac{|P_{mn}|}{\hbar$ — число квантов комбинационной частоты;
$m\cdot$ — число квантов частоты $ω 1$ , затраченных ( $P m n > 0$ ) или образованных ( $P m n < 0$ ) при возбуждении комбинационной частоты;
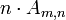$n\cdot$ — число квантов частоты $ω 2$ , затраченных ( $P m n > 0$ ) или образованных ( $P m n < 0$ ) при возбуждении комбинационной частоты.

Соотношения для трёхчастотного взаимодействия

Рассмотрим соотношения Мэнли — Роу в частном случае трёхчастотного взаимодействия. Пусть, например, комбинационной является разностная частота $ω 0 = ω 1 - ω 2$ . Тогда система имеет три частоты:

$\omega_0\$
$\omega_1\$
$\omega_2\$

В этом случае соотношения Мэнли — Роу принимают вид:

$\frac{P_{0,1}}{\omega_2}=\frac{P_{1,-1}}{\omega_0}=-\frac{P_{1,0}}{\omega_1}$

Обобщение для комбинации многих частот

Пусть источники или стоки квантов происходят на частотах

$\sum_{i=1}^N$

В этом случае будем иметь систему из $N$ соотношений:

$\sum_{m_1,m_2,\ldots,m_N}\frac{m_i\cdot$

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины