Главная » Самолетостроение » Физика » Энергия. Закон сохранения энергии

Энергия. Закон сохранения энергии

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.

С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени и в этом смысле является универсальным, то есть присущим системам самой разной физической природы. Другими словами, для каждой конкретной замкнутой системы, вне зависимости от её природы можно определить некую величину, называемую энергией, которая будет сохраняться во времени. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря различающимся для разных систем.

Однако в различных разделах физики по историческим причинам закон сохранения энергии формулируется по-разному, в связи с чем говорится о сохранении различных видов энергии. Например, в термодинамике закон сохранения энергии выражается в виде первого начала термодинамики.

Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то более правильным является его именование не законом, а принципом сохранения энергии.

С математической точки зрения закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.

Фундаментальный смысл закона

Согласно теореме Нётер каждому закону сохранению ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения энергии эквивалентен однородности времени, то есть независимости всех законов, описывающих систему, от момента времени, в который система рассматривается.

Вывод этого утверждения может быть произведён, например, на основе лагранжева формализма. Если время однородно, то функция Лагранжа, описывающая систему, не зависит явно от времени, поэтому полная её производная по времени имеет вид:

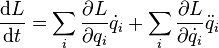
$\frac{{\rm$

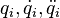Здесь $L(q_i,$ — функция Лагранжа, $q_i,$ — обобщённые координаты и их первые и вторые производные по времени соответственно. Воспользовавшись уравнениями Лагранжа, заменим производные $\frac{\partial$ на выражение $\frac{\rm$ :

$\frac{{\rm$

Перепишем последнее выражение в виде

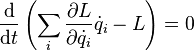
$\frac{\rm$

Сумма, стоящая в скобках, по определению называется энергией системы и в силу равенства нулю полной производной от неё по времени она является интегралом движения (то есть сохраняется).

Частные формы закона сохранения энергии

Классическая механика

Формулировка

В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом

Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.

Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть никуда.

Примеры

Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно. В случае математического маятника аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.

Вывод из уравнений Ньютона

Закон сохранения механической энергии может быть выведен из второго закона Ньютона, если учесть, что в консервативной системе все силы, действующие на тело,потенциальны и, следовательно, могут быть представлены в виде

$\vec$ ,

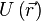где $U\left(\vec$ — потенциальная энергия материальной точки ( 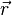$\vec$ — радиус-вектор точки пространства). В этом случае второй закон Ньютона для одной частицы имеет вид

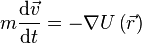$m\frac{\mathrm$ ,

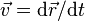где $m$ — масса частицы, $\vec$ — вектор её скорости. Скалярно домножив обе части данного уравнения на скорость частицы и приняв во внимание, что $\vec$ , можно получить

$m\vec$

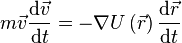
Путём элементарных операций это выражение может быть приведено к следующему виду

$\frac{\mathrm$

Отсюда непосредственно следует, что выражение, стоящее под знаком дифференцирования по времени, сохраняется. Это выражение и называется механической энергией материальной точки. Первый член в сумме отвечает кинетической энергии, второй — потенциальной.

Этот вывод может быть легко обобщён на систему материальных точек.

Термодинамика

В термодинамике исторически закон сохранения формулируется в виде первого принципа термодинамики:

Изменение внутренней энергии термодинамической системы при переходе её из одного состояния в другое равно сумме работы внешних сил над системой и количества теплоты, переданного системе, и не зависит от способа, которым осуществляется этот переход

или альтернативно:

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

В математической формулировке это может быть выражено следующим образом:

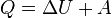$~Q=\Delta$ ,

где введены обозначения $Q$ — количество теплоты, полученное системой, $Δ U$ — изменение внутренней энергии системы, $A$ — работа, совершённая системой.

Закон сохранения энергии, в частности, утверждает, что не существует вечных двигателей первого рода, то есть невозможны такие процессы, единственным результатом которых было бы производство работы без каких-либо изменений в других телах.

Гидродинамика

В гидродинамике идеальной жидкости закон сохранения энергии традиционно формулируется в виде уравнения Бернулли: вдоль линий тока остаётся постоянной сумма

$\frac{v^2}{2}+w+gz$

Здесь введены следующие обозначения: 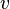$\$ — скорость потока жидкости, $\$ — тепловая функция жидкости, 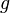$\$ — ускорение свободного падения, 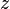$\$ — координата точки в направлении силы тяжести. Если внутренняя энергия жидкости не меняется (жидкость не нагревается и не охлаждается), то уравнение Бернулли может быть переписано в виде

$\frac{v^2}{2}+\int\frac{{\rm$

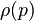где $\$ — давление жидкости, $\$ — плотность жидкости. Для несжимаемой жидкости плотность является постоянной величиной, поэтому в последнем уравнении может быть выполнено интегрирование:

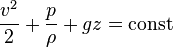
$\frac{v^2}{2}+\frac{p}{\rho}+gz$

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Дисциплины