Кинематика точки. Способы задания положения точки в пространстве.

Кинематика точки. Способы задания положения точки в пространстве.

При исследовании кинематических параметров мат.точки вводится 3 способа заданий ее положенияв пространстве, которые позволяютв разных системахкоординат в зависимости от поставленной задачи построить мат.модель объекта, оптимальную с точки зренияисследования движения объектов данной постановки и хорошо приспособленной для реализации вычислительной техники.

1.       Векторный способ задания движения точки.

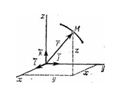
Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор  , проведенный из на­чала координат О в точку М (рис. 1). 

При движении точки М вектор   будет с течением времени изме­няться и по модулю, и по направлению.    является переменным вектором (вектором-функцией), зависящим от аргу­мента  t : 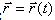.   Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор  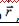 и найти положение движущейся точки.

Геометрическое место концов вектора 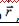 , т.е. годограф этого вектора, определяет траекторию движущейся точки.  Мгновенная скорость: ,  .

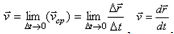2.       Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости ,   .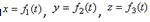

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t .Нетрудно установить зависимость между векторным и координатным способами задания движения.Разложим вектор 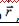  на составляющие по осям координат: 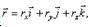где 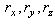 проекции вектора на оси;  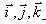– единичные векторы направленные по осям, орты осей.Так как начало  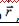 вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому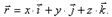  
Вектор скорости точки 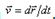 , учитывая, что  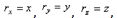 найдем:  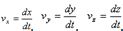 .Зная проекции скорости, найдем ее модуль и направление (т.е. углы 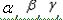, которые вектор  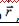 образует с координатными осями) по формулам ;   .

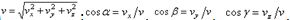 Примечание.Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы

3. Естественный способ задания движе­ния точки.

3. Естественный способ задания движе­ния точки.

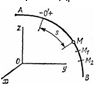
Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О' до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость 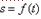. Уравнение выражает закон движения точки М вдоль тра­ектории.

Скорость точки есть первая производная по времени от закона движения: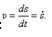

Ускорение: .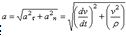

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.