Моменты силы

Момент силы относительно центра и оси.

Если физический объект имеет неподвижную точку А, то воздействие на него со стороны  другого объекта характеризуется вращательной составляющей его движения.

Материальная модель такого воздействия называется моментом силы F, относительно неподвижного центра А. Записывается (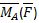 ) . Для того чтобы использовать при исследовании такого воздействия векторную алгебру считают, что момент силы относительно центра –вектор:

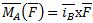(1)

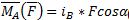(2)

Момент силы относительно оси.

Математическим моментом силы относительно оси называется проекция момента силы относительно центра А, лежащего на этой оси на данную ось. При решении задач в прямоугольной системе координат вводится понятие момента силы относительно осей x,y,z. В этом случае моменты силы определяются проекциями на соответствующую ось. Практически момент силы относительно оси равен моменту проекции этой силы на плоскость перпендикулярную оси относительно точки пересечения данной оси с плоскостью.

Лемма о параллельном переносе сил.

Силу, приложенную к физ. объекту  можно перенести параллельно самой себе в любую точку тела, добавив при этом момент данной силы относительно нового центра ее приложения.

Пара сил через точку момента А.

Если на тело действует 2 силы F1 uF2(вектора), которые F1=F2=F(вект) направлены в противоположные стороны и линии их действия параллельны, то система называется парой сил, ее нельзя преобразовать к 1 силе, ее воздействие на объект математически характеризуется моментом пары, которая является свободным вектором(не имеющим точку приложения) с величиной равной произведению одной из сил на расстояние между их линиями действия.

Лемма о параллельном переносе сил.

Пусть на А действует сила F, возьмем произвольную т. В и приложим к ней уравновешенную систему сил {F1,F2} такую, что F1=F2=F . Состояние тела Bне меняется.F1,F2- пара сил и ее момент: M{F1,F2}=-F*a=-F*h= . Т.о., сила F,приложенная к т.А перенесена параллельно самой себе в произвольную точку тела B,но при этом к телу добавлен ее момент относительно точки В.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.