Главная
»
Самолетостроение
»
Прикладная механика
»
Теорема о моменте равнодействующей (теорема Вариньона).
Теорема о моменте равнодействующей (теорема Вариньона).
Теорема о моменте равнодействующей (теорема Вариньона).
В этом пункте докажем теорему, которая широко применяется для решения задач, когда возникают трудности при вычислении моментов силы.
Если система сил приводится к равнодействующей, то момент равнодействующей относительно любого центра равен сумме моментов всех сил системы относительного того же центра.
Отметим, что к равнодействующей приводятся система сходящихся сил и система параллельных сил, для которых главный момент равен нулю.
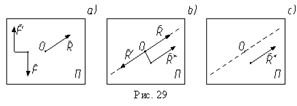
В общем случае к равнодействующей, не проходящей через центр приведения, приводится система сил, у которой главный вектор и главный момент взаимно ортогональны. Чтобы это показать, представим главный моментMO в виде пары (F,F'), лежащей в одной плоскости с главным вектором R(рис. 29, a). Пользуясь свойствами пары, трансформируем ее в пару (R*,R') , а затем повернем ее так, чтобы сила R' уравновесила главный вектор (рис. 29, b). Тогда останется одна сила R* , равная главному вектору по величине и направлению, но не проходящая через точку O (рис. 29, c). Момент равнодействующей относительно центра O равен моменту исходной пары, а он равен главному моменту или сумме моментов всех сил системы:
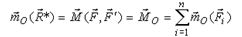
| (6) |
За центр приведения может быть выбрана любая точка тела, и поэтому выражения (6) справедливы для любого центра, когда система сил приводится к равнодействующей. Так доказана теорема Вариньона в самом общем виде.
Выражения (6) являются векторными для пространственной системы сил и алгебраическими для плоской системы сил, когда
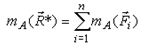
| (7) |
где A - любая точка плоскости, где лежат силы.
Теорема Вариньона может быть распространена и на моменты относительно осей, например, для оси OZ, так как момент силы относительно оси равен проекции на эту ось момента относительно центра на оси:
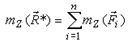
| (8) |
Итак, произвольная система сил приводится к одной силе и паре сил, причем сила является статическим инвариантом системы сил. Эту же систему сил можно привести к динамическому винту, в котором сила и момент пары будут статическими инвариантами. Кроме того, произвольная система сил может быть представлена в простейшем виде, как две силы, не лежащие в одной плоскости.
В частных случаях, когда система сил приводиться к одной силе или равнодействующей, выполняется теорема Вариньона о моменте равнодействующей, справедливая для векторов-моментов, алгебраических моментов и моментов силы относительно оси.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.