Общие теоремы динамики

Общие теоремы динамики.

1.       Теорема об изменении количества движения

а. Мат. точки

«Производная от количества движения мат. точки во времени равна главному вектору сил, приложенных к материальной точке» Количеством движения называется вектор, который представляет собой вектор скорости, измененный в n раз. Эта теорема используется при исследовании мат. Точки, когда превалирует поступательная составляющая движения, а вращательной составляющей можно пренебречь. .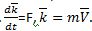

В интегральной форме:

б. Системы мат. точек

Количество движения для систем мат.точек 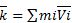 .«Первая производная от количества движения системы мат.точек во времени равна главным векторам внешних сил, приложенных к точкам системы». В интегральной форм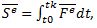е: , где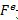 –внешние силы.

2.       Теорема о движении центра масс системы материальных тел.

 Центр масс механической системы движется как точка, масса которой равна массе всей системы M=Σm_i, к которой приложены все внешние силы системы: 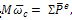или в координатной форме: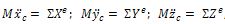

где 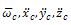  - ускорение центра масс и его проекции на оси декартовых координат;  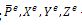внешняя сила и ее проекции на оси декартовых координат.

3.       Теорема об изменении кинетического момента.

а.Мат.точки

Кинетическим моментом (моментом количества движения ,L) называется вектор 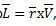,где r-радиус-вектор исследуемой точки относительно выбранного неподвижного центра О. Эта теорема используется в случае, если необходимо учесть вращательную составляющую движения объекта. В случае, если объект находится в сложном движении, которое составляли мат.модель, можно представить состоящим из 2х движений: поступательного и вращательного.(тогда будет необходимо использовать 2 теоремы : теорема об изменении количества движения, теорема об изменении кинетического момента).

«Первая производная от кинематического момента мат. точки равна главному моменту сил, приложенных к мат. Точке относительно того же центра О»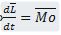

б. Система мат. Точек(тел)

«Первая производная от кинетического момента системы материальных точек (тел) относительно выбранного центра во времени равна моменту главного вектора внешных сил, приложенных к точкам механической системы относительно того же центра О»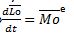

При исследовании движения механических объектов когда существенна вращательная составляющая движения часто математическая модель строится на основе следствия из этой теоремы. Следствие: Если ммоент главного вектора сил, приложен к мат.точке относительно выбранного центра О и не равен 0, то объект вращается с постоянной угловой скоростью.

4.       Теорема об изменении кинетической энергии.

«Изменение кинетической энергии мат.точки за некоторый интервал времени равно сумме работ всех сил, приложенных к мат.точке на их перемещение за тот же интервал времени.»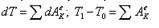 style=width: 162.75pt; height: 15.75pt; visibility: visible;>

В общем случае работа - скалярное произведение - векторы: A=F*r ( где r - перемещение точки). Часто при исследовании динамических параметров объекта для получения более простых аналитических выражений используется понятие мощности. 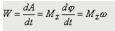style=width: 122.25pt; height: 19.5pt; visibility: visible;> . Также выражение силы расписывается: A=F*r*cosα. При этом каждая сила при перемещении тела имеет свое перемещение.

Кинетическая энергия определяется в зависимости от вида движения объекта и характеризует динамику этого движения с учетом инертности тела.

а. Если тело находится в поступательном движении: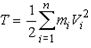

б. Вращательное движение объекта.Инертность характеризуется моментом инерции объекта относительно выбранного центра по некоторой оси L или координатной плоскости. Относительно центра - полярный момент Io, относительно оси - осевой Iл, Относительно плоскости – планарный Ixy . В общем случае момент инерции, характеризующий его динамику, определяется относительно координатных осей и начала координат. Кинетическая энергия для вращательного движения: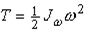

в. Сложное движение : 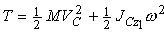 ,где C-центра масс соответствующего объекта.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.