Приведение произвольной СС к простейшему виду.

Приведение произвольной СС к простейшему виду.

До формулировки и доказательства теоремы дадим понятия главного вектора и главного момента системы сил.

Главным вектором системы сил называют вектор, равный сумме всех сил системы:

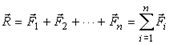(2)

Главным моментом системы сил относительно центра называют вектор, равный сумме моментов всех сил системы относительно центра:

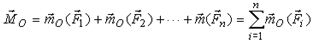(3)

Сформулируем основную теорему статики.

Произвольная система сил, приложенная к твердому телу, эквивалентна одной силе, приложенной в центре приведения и равной главному вектору, и одной паре сил, момент которой равен главному моменту относительно центра приведения:

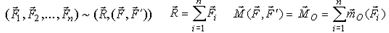(4)

Докажем теорему. Пусть к твердому телу приложена произвольная система сил (F₁, F₂, ..., F_n). Какую либо точку тела выберем за центр приведения и обозначим буквой O. Следуя лемме, силы системы переносим в эту точку и получаем систему пар сил и пучок сил в центре приведения. Складывая все силы пучка и пары сил, получаем одну силу в центре приведения и одну пару сил. Силы пучка по величине и направлению равны силам исходной системы, поэтому полученная сила равна главному вектору системы R. Моменты пар равны моментам соответствующих сил относительно центра O, поэтому момент полученной пары сил (F,F') равен главному моменту системы M_O. Теорема доказана.

Заметим, что при параллельном переносе сил к центру приведения не изменились ни модули, ни направления сил, поэтому главный вектор не зависит от выбора центра приведения. Главный вектор является инвариантом (неизменной величиной) данной системы сил. В отличие от главного вектора, главный момент зависит от выбранного центра приведения и не является инвариантом.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.