Главная
»
Самолетостроение
»
Прикладная механика
»
Условия равновесия произвольной СС в геометрической и аналитической формах.
Условия равновесия произвольной СС в геометрической и аналитической формах.
Условия равновесия произвольной СС в геометрической и аналитической формах.
Для доказательства условий равновесия воспользуемся основной теоремой статики:
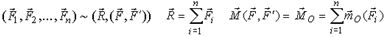
| (1) |
Сформулируем условия равновесия, а затем их докажем.
Для равновесия твердого тела под действием произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю:
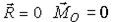 | (2) |
Необходимость условий (2) сразу следует из (1). При выполнении (2) (R,(F,F')) ~ 0 и (F1, F2, ..., Fn) ~ 0. Достаточность условий равновесия докажем методом от противного. Предположим, что не выполняются оба условия или хотя бы одно из них, а тело находится в равновесии. Но в этих случаях система сил приводится к двум силам, не лежащим в одной плоскости, или к одной силе, или к одной паре сил, под действием которых твердое тело не может быть в равновесии. Следовательно, наше предположение не верно, а верны условия равновесия (2), достаточность которых доказана.
Условия равновесия (2) являются условиями равновесия в геометрической или в векторной форме. Эти условия широко используются в теоретических доказательствах, однако при решении практических задач они не применяются из-за сложности построения силового и моментного многоугольников в пространстве.
Для получения условий равновесия в аналитической или в координатной форме свяжем с поверхностью Земли или основанием систему координат OXYZ. Центром приведения выберем начало координат O. Спроектируем на оси координат оба векторных выражения в (2). При проектировании учтем, что момент силы относительно оси равен проекции момента относительно центра на оси. В результате получим шесть аналитических выражений:
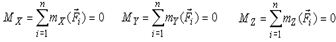
| (3) |
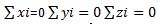 | |
Эти выражения представляют математическую запись условий равновесия произвольной системы сил в аналитической форме.
Для равновесия произвольной системы сил необходимо и достаточно, чтобы три суммы проекций всех сил на оси координат и три суммы моментов всех сил относительно осей координат равнялись нулю.
Если условия равновесия (3) содержат известные и неизвестные силы конкретной задачи, то их называют уравнениями равновесия.
Следует отметить, что при составлении уравнений равновесия за центр приведения может быть выбрана любая другая точка, так как при выборе нового центра приведения O1получим, что MO1 = mO1(R) + MO. И если для центра O выполняются условия (2), то для любого другого центра приведения, например O1, будет R = 0 и MO1 = 0.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.