Адаптивная дискретизация аналоговых сигналов.

47. Адаптивная дискретизация

При адаптивной дискретизации отсчетные точки t_i в от­личие от равномерной выборки не образуют периодической последовательности. В процессе обработки сигнала отбираются лишь те точки t_i (минимально необходимое число) и соот­ветствующие выборки x(f), на основании которых можно вос­становить исходный сигнал   с заданной точностью ε₀.

Таким образом, в процессе адаптивной дискретизации вы­деляется минимальное число выборок x(t), называемых су­щественными, которые с заданной точностью отображают непрерывный сигнал.

В связи с тем, что отсчетные точки при адаптивной диск­ретизации в общем случае произвольно размещены на вре­менной оси, необходимо иметь информацию о значении мо­ментов опроса t_i  или о длинах соответствующих отрезков ∆t_i.

В настоящее время существует значительное число спо­собов и алгоритмов адаптивной дискретизации. Среди них можно выделить две группы:

•  способы, при которых производится сравнение сигнала x(t) с приближающей функцией P(t, формируемой в процес­се обработки сигнала x(t) с учетом его характеристик;

•  способы, при которых осуществляется сравнение сиг­нала с некоторыми эталонными фиксированными функциями

Значительный интерес представляют способы и алгорит­мы адаптивной дискретизации, относящиеся к первой группе, так как при этом обеспечивается наиболее эффективное уст­ранение избыточности отсчетов и соответственно минимиза­ция описания исходного сигнала. В общем виде процедура адаптивной дискретизации в этом случае сводится к поиску на каждом из отрезков (t_i, t_i+1) некоторой функции принято­го типа, наилучшим образом представляющей исходную фун­кцию x(t) в соответствии с заданным критерием уклонения.

Адаптивная дискретизация может быть организована та­ким образом, что на отрезках (t_i t_i+1) постоянной длины мо­гут меняться тип и порядок (степень) приближающих функ­ций или при неизменном типе и порядке приближающей фун­кции изменяется длина отрезка. Возможна адаптация и по двум этим показателям.

В практических применениях наибольшее распростране­ние нашли алгоритмы адаптивной дискретизации с адапта­цией по длинам отрезков (t, t_i+1) , использующие алгебраи­ческие полиномы нулевой и первой степени. Рассмотрим про­стейшие алгоритмы адаптивной дискретизации при оценке точности приближения (воспроизведения) по критерию наи­большего отклонения.

Экстраполяционные способы адаптивной дискретизации полиномом нулевой степени относительно t содержат опера­цию сравнения текущего значения сигнала x(t) со значением предшествующей выборки x(t_i) сигнала.

Пусть приближающая функция P(t_, на отрезке (t_i, t_i+1) выбирается следующим образом:

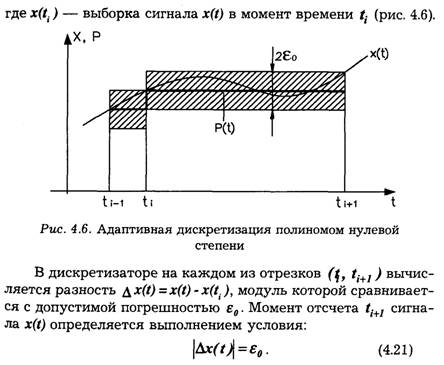
В устройствах адаптивной дискретизации с полиномами нулевой степени этот способ применяется наиболее часто.

При использовании адаптивной дискретизации с полино­мами первой степени приближающая функция P(t, на отрез­ке (t_i, t_i+1) может иметь вид:

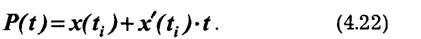
В устройстве дискретизации на каждом из отрезков (t_i, t_i+1) генерируется приближающая функция вида (4.22) и вычисляется ∆x(t). Моменты отсчета определяются выпол­нением условия:

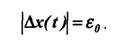
В данном случае определение приближающих функций на отрезках (t_i, t_i+1) связано с дифференцированием сигнала.

Следует заметить, что аппаратная реализация алгорит­мов адаптивной дискретизации с полиномами первой степени достаточно сложна.

При адаптивной дискретизации с эталонными приближа­ющими функциями исходный сигнал x(t) сравнивается с на­бором эталонных сигналов {f_k(t)}, поступающих от специ­ального генератора. По результатам сравнения определяются моменты отсчетов сигнала.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.