Равномерная дискретизация. Теорема Котельникова. Представление сигнала рядом Котельникова.

Равномерная дискретизация. Теорема Котельникова

При равномерной дискретизации шаг ∆t и частота отсче­тов являются постоянными величинами. Точки отсчетов в этом случае равномерно размещены по оси t.

Устройства, с помощью которых проводится дискретиза­ция сигналов, носят название дискретизаторов. На рис. 4.2. изображена функциональная схема дискретизатора.

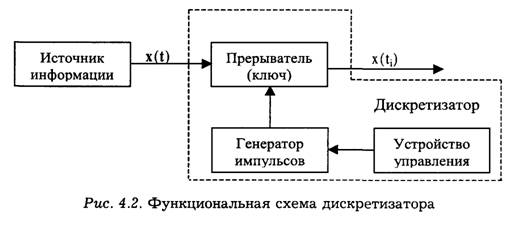
Дискретизатор можно рассматривать как прерыватель ис­ходного сигнала x(t). Генератор импульсов выдает на вход пре­рывателя некоторую последовательность импульсов, в ре­зультате чего входной сигнал x(t) преобразуется в последо­вательность дискретных выборок сигнала x(t). Работа гене­ратора импульсов определяется устройством управления. В случае равномерной дискретизации частота импульсов, по­ступающих от генератора, является неизменной.

В. А. Котельниковым доказана теорема для функций с ограниченным (финитным) спектром (теорема отсчетов), ко­торая формулируется следующим образом: если наивысшая частота в спектре функции x(t) меньше, чемƒ_m, то функ­ция x(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 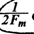секунд.

Интерполяционный ряд вида (4.9) носит название ряда Котельникова. (В иностранной литературе этот ряд связыва­ют с именами Найквиста и Шеннона.)

Пусть сигнал, описываемый непрерывной функцией вре­мени x(t), имеет ограниченный спектр, т. е. преобразование Фурье:

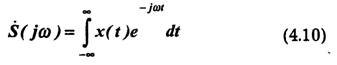
Подставим выражение (4.14) в формулу (4.11), изменив при этом знак при п с учетом, что суммирование проводится по всем отрицательным и положительным значениям п.Кро­ме того, учитывая сходимость ряда и интеграла Фурье, изме­ним порядок операций интегрирования и суммирования:

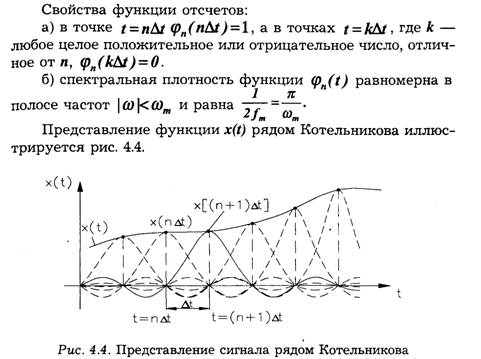
При выводе (4.9) предполагалось, что x(t) удовлетворяет условиям Дирихле. Это не дает возможности использовать полученный результат для функций, не стремящихся к нулю при t →∞, или для функций, не интегрируемых на интерва­ле (а, в).

Теорема Котельникова относится к сигналам с ограни­ченным спектром. Реальные сообщения имеют конечную дли­тельность. Спектр таких сигналов не ограничен, т. е. реаль­ные сигналы не соответствуют модели сигнала с ограничен­ным спектром, и применение теоремы Котельникова к реаль­ным сигналам связано с погрешностями при восстановлении сигналов по формуле (4.9) и неопределенностью выбора шага дискретизации (4.16) или частоты отсчетов F₀=2f_m.

Приведенные соображения свидетельствуют, что приме­нение теоремы Котельникова к реальным сигналам вызывает определенные трудности в том случае, если теорема рассмат­ривается как точное утверждение. Для практических усло­вий, однако, идеально точное восстановление функций не тре­буется, необходимо лишь восстановление с заданной точнос­тью. Поэтому теорему Котельникова можно рассматривать как приближенную для функций с неограниченным спектром.

Практически всегда можно определить наивысшую час­тоту спектра f_m так, чтобы хвосты функции времени, обус­ловленные отсеканием частот, превышающих f_m, содержали пренебрежимо малую долю энергии по сравнению с энергией исходного сигнала x(t). При таком допущении для сигнала дли­тельностью Т с полосой частот общее число независимых па­раметров [т. е. значений x(n∆t) ], которое необходимо для пол­ного задания сигнала, очевидно, будет:

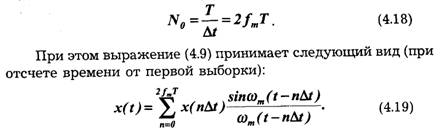
Величина N₀ представляет собой число степеней свобо­ды сигнала x(t), так как даже при произвольном выборе зна­чений x(r∆t) сумма вида (4.19) определяет функцию, удов­летворяющую условиям заданного спектра и заданной дли­тельности сигнала.

Параметр B=N₀, который широко применяется в систе­мах передачи информации, называют базой сигнала.

Представление сигналов в виде ряда Котельникова поло­жено в основу построения систем передачи информации с временным уплотнением. Смысл временного уплотнения со­стоит в том, что в интервале времени между двумя соседни­ми отсчетами одного сигнала можно передавать отсчеты дру­гих сигналов. Формирование такого группового сигнала пока­зано на рис. 4.5.

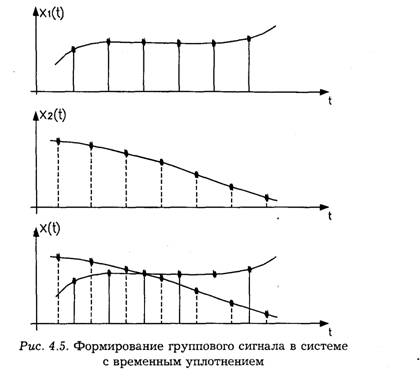
В заключение данного параграфа заметим, что хотя тео­рема Котельникова базируется на модели сигнала с ограни­ченным спектром, она имеет большую теоретическую и прак­тическую ценность. Поэтому представление сигналов рядом Котельникова наиболее широко применяется в технике пре­образования, передачи и обработки информации.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.