Базисные функции в задаче восстановления дискретизированных сигналов.

44.        Базисные функции в задаче восстановления дискретизированных сигналов.

Задачи дискретизации сигналов, особенно адаптивной, в математическом плане достаточно близки к задачам равно­мерных и среднеквадратических приближений функций. Фор­мулировка задачи дискретизации может быть следующей.

Для данной функции x(t), определенной на отрезке [a,в], найти функцию Р(t,(или V(t)), для которой число точек раз­биения t_i отрезка минимально и ε(t )≤ ε₀. Здесь ε₀ — допус­тимое значение погрешности, ε (t ) — оценка отклонения x(t) от P(t) (или V(t) в  соответствии с принятым критерием.

Функции P(t) называют приближающими.

На практике при решении задач дискретизации сигналов выбор типа базисных (приближающих, воспроизводящих) функций в основном определяется требованиями ограниче­ния сложности устройств (программ) дискретизации и вос­становления сигналов.

Задачи восстановления дискретизированных сигналов в общем случае аналогичны задачам интерполирования функ­ций. При восстановлении исходного сигнала x(t)совокупность выборок x(t) ставится в соответствии с некоторым обобщен­ным многочленом:

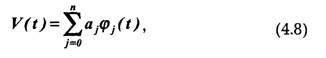
значения которого в точках отсчета t- совпадают со значения­ми функции x(t).

Иногда, кроме того, требуют совпадения производных до n-го порядка, n = 1,2,3...

Воспроизводящие функции V(t) обычно совпадают с при­ближающимися P(t,, хотя в общем случае они могут и отли­чаться от них.

Основные типы функций, применяемые в задачах диск­ретизации и восстановления сигналов, следующие: ряд Фу­рье, ряд Котельникова, полиномы Чебышева, полиномы Ле-жандра, степенные полиномы, функции Уолша и др.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.