Соотношение между спектральной плотностью и ковариационной функцией случайного процесса. Белый шум.

25. Соотношение между спектральной плотностью и ковариационной функцией случайного процесса. Белый шум

С одной стороны, скорость изменения x(t) во времени определяет ширину спектра. С другой стороны, скорость из­менения x(t) определяет ход ковариационной функции. Оче­видно, что между W_x(ω) и К_х(τ) имеется взаимно однознач­ная связь.

Теорема Винера-Хинчина утверждает, что К_х(τ) и W_X(ω) связаны между собой преобразованиями Фурье:

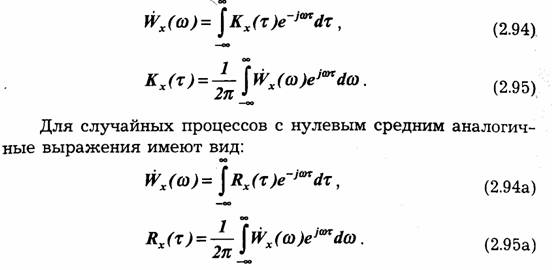
Из этих выражений вытекает свойство, аналогичное свой­ствам преобразований Фурье, установленным в п. 2.9 для де­терминированных сигналов: чем шире спектр случайного процесса, тем меньше интервал корреляции и, соответ­ственно, чем больше интервал корреляции, тем уже спектр процесса.

Для белого шума с бесконечным и равномерным спект­ром корреляционная функция равна нулю для всех значений τ, кроме τ = 0, при котором Rx(0) обращается в бесконеч­ность. Подобный шум, имеющий игольчатую структуру с бес­конечно тонкими случайными выбросами, иногда называют дельта-коррелированным процессом. Дисперсия белого шума бесконечно велика. Если спектр Wx(ω) ограничен сверху частотой ω _в, то такой процесс называется квазибе­лым шумом.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.