Главная
»
Самолетостроение
»
Теория информационных процессов и систем
»
Скорость передачи информации и пропускная способность дискретных каналов с помехами.
Скорость передачи информации и пропускная способность дискретных каналов с помехами.
59. Скорость передачи информации и пропускная способность дискретных каналов с помехами.
Отличительной особенностью рассмотренных ранее каналов без помех является то, что при выполнении условия теоремы Шеннона количество принятой информации на выходе канала всегда равно количеству информации, переданной от источника сообщений.
При этом, если на вход канала поступил сигнал ui, то на выходе возникает сигнал vi, вполне однозначно определяющий переданный сигнал ui. Количество информации, прошедшее по каналу без помех в случае передачи ui и приема vi, равно количеству информации, содержащейся в сигнале ui:
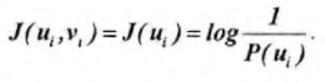
Здесь величина вероятности P(ui) характеризует ту неопределенность в отношении сигнала ui, которая существо вала до его передачи. После приема vi, в силу однозначного соответствия между ui и vi, неопределенность полностью устраняется.
Иное положение имеет место в каналах, где присутствуют различного рода помехи. Воздействие помех на передаваемый сигнал приводит к разрушению и необратимой потере части информации, поступающей от источника сообщения. Поскольку в канале с помехами принятому сигналу vi может соответствовать передача одного из нескольких сигналов u, то после приема остается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие между u и v носит случайный характер, поэтому степень неопределенности характеризуется условной апостериорной вероятностьюP(ui/vi), причем всегда P(ui/vi)<1. Количество информации, необходимое для устранения оставшейся неопределенности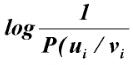 , очевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда в соответствии с формулой (6.9) количество принятой информации определяется как разность:
, очевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда в соответствии с формулой (6.9) количество принятой информации определяется как разность:
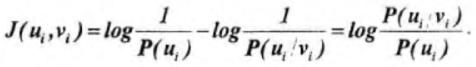
Для того чтобы определить пропускную способность, необходимо максимизировать J(u,v) = H(v)-H(vju). При заданной вероятности ошибки, величина H(v/u) — постоянная, а максимум следует искать, изменяя H(v).Энтропия сигнала H(v), имеет максимальное значение Hg(v) = 1 в случае равновероятных сигналов, когда P(v1)=P(v2)=0.5.
Подставляя выражения в формулу, получим следующее выражение для пропускной способности двоичного симметричного канала:
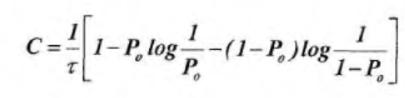
Для многопозиционного симметричного канала при mu=mv=m>2:
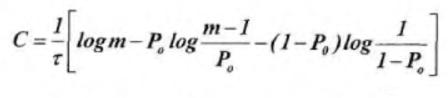
рис. 6.2 приведена зависимость С от вероятности ошибки для двоичного канала .
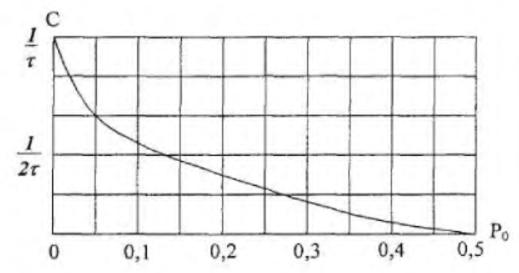
Рис. 6.2. Зависимость пропускной способности двоичного канала от вероятности ошибки Р0
Увеличение вероятности ошибки Р0 приводит к снижению пропускной способности, которая становится равной нулю при Р0 =0,5. В этом случае полностью исчезает какая-либо зависимость между передаваемыми и принятыми сигналами: P(v1/u1)=P(v2/u1)=1/2 и P(v1/u2)=P(v2/u2)=1/2, значение Р0 = ½ для бинарного канала является предельным.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.