Спектральная плотность мощности случайного процесса. Энергетический спектр сигнала.

24.    Спектральная плотность мощности случайного процесса

Подразумевая под случайным процессом множество (ан­самбль) функций времени, необходимо иметь в виду, что фун­кциям, имеющим различную форму, соответствуют различ­ные спектральные характеристики. Усреднение комплексной спектральной плотности, введенной в п. 2.5, по всем функци­ям приводит к нулевому спектру процесса (при M[x(t)]=0)из-за случайности и независимости фаз спектральных состав­ляющих в различных реализациях. Можно, однако, ввести понятие спектральной плотности среднего квадрата слу­чайной функции, поскольку значение среднего квадрата не зависит от соотношения фаз суммируемых гармоник. Если под случайной функцией x(t) подразумевается электрическое напряжение или ток, то средний квадрат этой функции можно рассматривать как среднюю мощность, выделяемую сопротив­лением 1Ом. Эта мощность распределена по частотам в неко­торой полосе, зависящей от механизма образования случай­ного процесса. Спектральная плотность средней мощности представляет собой среднюю мощность, приходящуюся на 1Гц при заданной частоте ω . Размерность функции W(ω), явля­ющейся отношением мощности к полосе частот, есть:

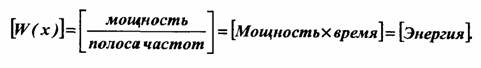
Спектральную плотность случайного процесса можно найти, если известен механизм образования случайного процес­са. Здесь мы приведем только определение общего характера.

Выделив из ансамбля какую-нибудь реализацию x_k (t) и ограничив ее длительность конечным интервалом у, можно применить к ней обычное преобразование Фурье и найти спек­тральную плотность Х_КТ(ω). Тогда энергию рассматриваемо­го отрезка реализации можно вычислить с помощью форму­лы (2.73):

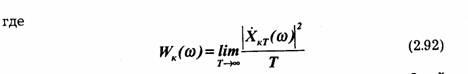
представляет собой  спектральную плотность средней мощности ê-й. реализации.

В общем случае величина W_k(ω) должна быть усреднена по множеству реализаций. Ограничиваясь в данном случае рас­смотрением стационарного и эргодического процесса, можно считать, что найденная усредненная по одной реализации фун­кция W_k (ω) характеризует весь процесс в целом. Опуская ин­декс к, получаем окончательное выражение для средней мощ­ности случайного процесса:

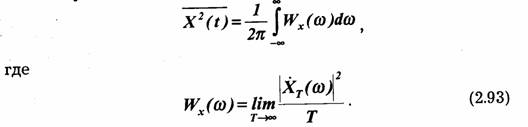
Энергетический спектр, естественно, не несет в себе све­дений о фазовых соотношениях. Восстановить реализации процесса как функции времени по энергетическому спек­тру нельзя.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.