Распределение мощности в спектре периодического сигнала. Ширина спектра сигнала, учитывающая 95…98% мощности сигнала.

Распределение мощности в спектре периодической последовательности импульсов.

Полная мощность периодической последовательности импульсов определяется суммой средних мощностей, выделяемых постоянной составляющей и гармониками.

Если гармонику представить током, то:

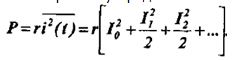
Черта над функцией означает усреднение значения функции от времени; r – сопротивление.

12Йі=PОЈP>   12PОЈ>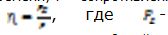 мощность ограниченного спектра;                            P- мощность колебаний.

Ширина спектра и длительность сигнала

При рассмотрении вопроса о сжатии и растяжении сигнала стало ясно, что чем уже сигнал, тем более широкий у него спектр. Обычно как сигнал, так и его спектр, не бывают строго ограничены по времени или по частоте. Поэтому необходимо определить понятия длительность сигнала и ширина его спектра. При этом обычно используют два подхода:

• энергетический;
• информационный.

При энергетическом подходе длительность сигнала или ширину его спектра определяют по заданной доле от полной энергии сигнала. Так, например, для сигнала в виде прямоугольного импульса длительностью t спектральная плотность имеет бесконечно широкий спектр, однако анализ показывает, что первый лепесток спектра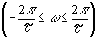 содержит 90% от полной энергии импульса, а сумма первого и второго 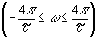уже 95%. Аналогично можно рассуждать и о длительности бесконечно длящегося сигнала с конечной энергией.

При информационном подходе важное значение имеет форма сигнала: чем шире взята за основу условная ширина его спектра, тем ближе по форме к исходному может быть воспроизведенный по ограниченному спектру сигнал. Иногда ширину спектра определяют по уровню 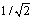 от максимального значения. Для колоколообразных импульсов принята величина е^-1/2=0,606 от максимума. Ширина спектра и длительность сигнала взаимосвязаны. Для выявления этой связи определяют так называемые эффективныедлительность и ширину спектра, которые вычисляют с помощью следующих соотношений:

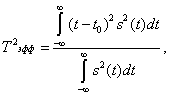
где 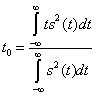 середина импульса;

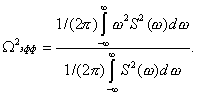
Полная длительность сигнала равна 2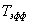, а полная ширина спектра , включая и отрицательные частоты, 2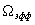, Произведение длительности на полосу равно:

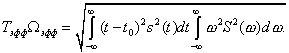
Произведение 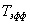*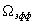зависит от формы сигнала, но не может быть меньше 0.5(только для импульсов гауссовой формы это произведение равно 0.5). Не для всех сигналов данные интегралы имеют смысл(сходятся). Для определения 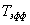и 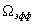 необходимо, чтобы функция s(t) убывала бы быстрее, чем 1/t, а функция S( w ) быстрее, чем 1/ w .

Для сигналов, не удовлетворяющих этим условиям, и применяют энергетический, либо информационный критерий, но следует помнить, что с уменьшением длительности сигнала ширина его спектра увеличивается, т.е. произведение длительности на ширину спектра для данного типа сигнала величина постоянная

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.