Теорема Шеннона для дискретного канала с помехами.

Для дискретных каналов с помехами Шеннона доказал теорему:

«Если производительность источника Rи ≤ C-ξ , где ξ – сколь угодно малая величина, то существует способ кодирования, позволяющий передавать все сообщения источника  со сколь угодно малой вероятностью ошибки».

С – пропускная способность.

При Rи ≥ C такая передача невозможна.

Т. Шеннона доказывает, что наличие помех и ошибок в канале, не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок, а лишь ограничивает максимальную скорость передачи информации.

Из теоремы не вытекает способ декодирования.

Рассмотрим ситуацию:

Кодом МТК-2 передается буква “П”-> 01101(n=5)

В канале связи возникают ошибки. P – вероятность ошибки. Предположим, что при передачи q=0 ошибок вероятность правильного приема 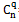=C(q,n)=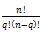; C(0,5)=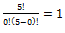 

C(1,5)=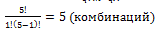 

01101 –> 11101(Я); 00101(Х); 01001(Л); 01111(Ж); 01100(И).

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.