Узкополосный сигнал. Характерный вид узкополосного сигнала. Комплексная огибающая узкополосного сигнала.

34. Узкополосный сигнал

Современное состояние техники характеризуется непре­рывным совершенствованием способов передачи информации. Изыскиваются новые виды сигналов и новые способы их об­работки.

Рассмотренные в предыдущих параграфах модулирован­ные колебания являются лишь простейшими видами сигна­лов. В настоящее время широко применяются сигналы, полу­ченные в результате модуляции амплитуды и частоты (или фазы) колебания по очень сложному закону.

В любом случае предполагается, что заданный сигнал s(t) представляет собой узкополосный процесс. Это означает, что все спектральные составляющие сигнала группируются в от­носительно узкой, по сравнению с некоторой центральной ча­стотой 0)_д, полосе.

При представлении подобных сигналов в форме:

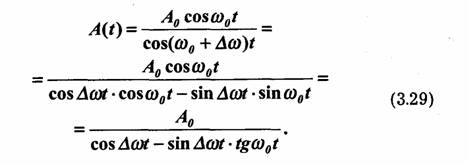
Из этого примера видно, что при нерациональном выборе ψ (t) (ω t вместо ω ₀t) очень усложнилось выражение для A(t), причем эта новая функция A(t) по существу не является оги­бающей в общепринятом смысле, так как она может пересе­кать кривую s(t) (вместо касания в точках, где s(t) имеет максимальное значение). Оперирование подобной огибающей не имеет смысла, а в некоторых случаях и недопустимо, так как может привести к ошибочным практическим выводам.

Неопределенности можно избежать при представлении A(t) и ψ (t) с помощью следующих соотношений:

В данном случае получается простейшая огибающая в виде линии, касательной к исходной функции в точках ее мак­симума и соединяющей эти точки кратчайшим путем. Это свой­ство выражения (3.30) сохраняется и для сложного сигнала, если выполняется условие медленности изменения огибаю­щей, т. е. если речь идет об узкополосном сигнале.

Если исходный сигнал представляет собой сумму спект­ральных составляющих

Нетрудно установить связь между спектрами функций s(t) и s₁(t). Так как при преобразовании гармонического ко­лебания по Гильберту его амплитуда остается неизменной, то очевидно, что по модулю спектральная плотность S₁(ω) со­пряженной функции s₁(t) не может отличаться от исходной функции s(t). Фазовая же характеристика спектра S1(ω) от­личается от ФЧХ спектра S(ω). Из сопоставления (3.36) и (3.37) непосредственно вытекает:

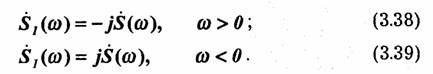
Вследствие изменения ФЧХ сопряженная функция s₁(t) по своей форме может сильно отличаться от исходной функ­ции s(t).

После того как найдена сопряженная функция s₁(t), можно с помощью выражений (3.30), (3.31) найти огибающую A(t), полную фазу ψ (t) и мгновенную частоту узкополосного сиг­нала:

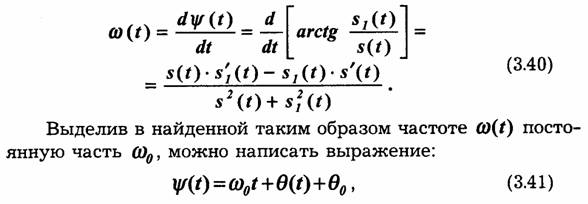
в котором Ө(t) не содержит слагаемого, линейно меняющего­ся от времени. Тем самым устраняется произвол в выборе средней частоты сигнала ω ₀ и соответственно функции Ө(t).Характерный вид такого узкополосного сигнала приведен на рис. 3.10.

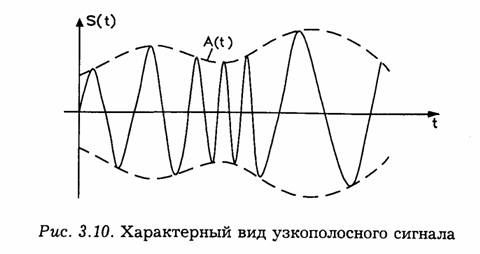
В заключение данного параграфа рассмотрим еще один способ представления сигналов, который в настоящее время достаточно широко применяется в теории передачи инфор­мации.

Если задан физический сигнал s(t) в виде действитель­ной функции, то соответствующий ему комплексный сигнал представляется в форме:

Комплексный сигнал, определяемый выражениями (3.42) и (3.43), называется аналитическим сигналом.

В теории электрических цепей принято представлять гар­монические колебания в комплексной форме записи. Аналитический сигнал является обобщением такой формы записи на негармонические колебания. Пусть задан физический сигнал:

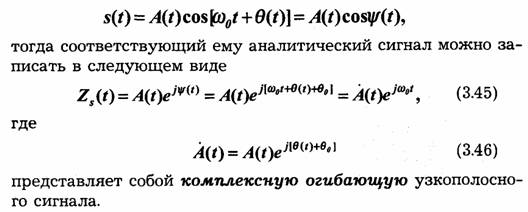
Модуль комплексной огибающей, равный A(t), содержит информацию только об амплитудной модуляции колебания, а фазовый множитель e^jө(t) — только об угловой модуляции. В целом же произведение A(t)e^jө(t) содержит полную информа­цию о сигнале s(t) (за исключением несущей частоты ω ₀, ко­торая предполагается известной).

Это свойство комплексной огибающей, позволяющее при анализе узкополосных сигналов исключить из рассмотрения частоту ω ₀, придает важное значение понятию аналитичес­кий сигнал. В некоторых устройствах обработки сигналов при­ходится иметь дело с совокупностью двух функций времени, сопряженных по Гильберту, т. е. с аналитическим сигналом как с физическим процессом.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.