Непериодические сигналы. Представление непериодической функции. Особенности спектра непериодической функции.

Непериодические сигналы.

В реальных системах передачи всегда действуют непериодические сигналы, так как все сигналы имеют конечную длительность.

Пусть задан сигнал в виде функции времени, удовлетворяющей условиям Дирихле во всяком конечном интервале и, кроме того, абсолютно интегрируемой. 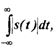 ls(t)l-абсолютное значение функции s(t).

Для проведения гармонического анализа непер.ф-ии поступим след образом: превратим эту функцию с произв периодом T.

Тогда для этой новой функции применимо разложение в ряд Фурье.

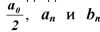
входящие в выражение коэффициенты

Устремляя T к бесконечности, в пределе получим бесконечно малые амплитуды гармонических составляющих.

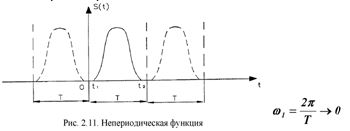
Расстояние м-у спектр линиями, равное частоте w, становится бесконечно малым, а спектр сплошным.

Отсюда след., что при гармоническом анализе непериодич. ф-ии получается сплошной спектр, состоящий из бескон. большого количества гармоник с бескон. малыми амплитудами.

Эта пара выражений называется прямым и обратным преобраз. Фурье.

Вывод:огибающая сплошного спектра(модуль спектр плотности) непер ф-ии и огиб-я линейчатого спектра переод. ф-ии(получ из непер. путем продолжения ее с периодом T) совпадают по форме и отличаются только масштабом.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.