Периодические сигналы. Пример периодического сигнала. Спектр периодической функции

Периодические сигналы.

Простейшим периодическим сигналом является гармоническое колебание    (тока,    напряжения,    заряда,    напряженности поля), определяемое законом:

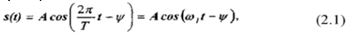
при -∞<t<+∞.

Здесь A, Т, ω₁, ψ — постоянные амплитуда, период, частота и

фаза.

Гармоническое колебание, определяемое выражением (2.1), иногда удобно представлять в одной из следующих комплексных форм:

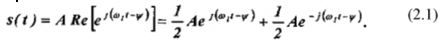
Первой из этих форм соответствует векторное представление, изображенное на рис. (2.2а). а второй форме — на рис. (2.26).

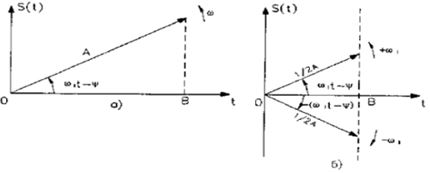
Любой сложный периодический сигнал может быть представлен в виде суммы элементарных гармонических сигналов, представленных при помощи ряда Фурье.

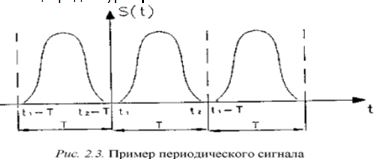
Подобный сигнал может быть представлен рядом Фурье в тригонометрической или комплексной формах:

Совокупность коэффициентов An называется спектром сигнала и полностью определяет этот сигнал.

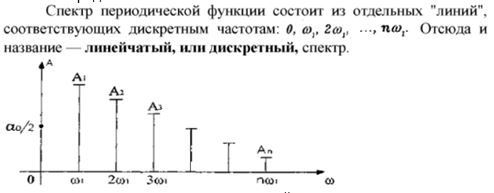
Значение рядов Фурье в современной технике очень велико. Наибольшее распространение представление сигналов рядом Фурье получило при исследовании процессов прохождении сигналов через электрическую цепь.

Для нахождения выходного сигнала достаточно учесть какие амплитудные и фазовые изменения претерпевает каждая гармоническая составляющая при прохождении через рассматриваемую систему.

Сигнал на выходе будет иметь вид:

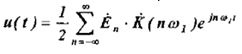
1.      Спектры некоторых периодических сигналов.

1)     Периодическая последовательность прямоугольных импульсов.

Рассмотрим спектры периодической последовательности прямоугольных импульсов.

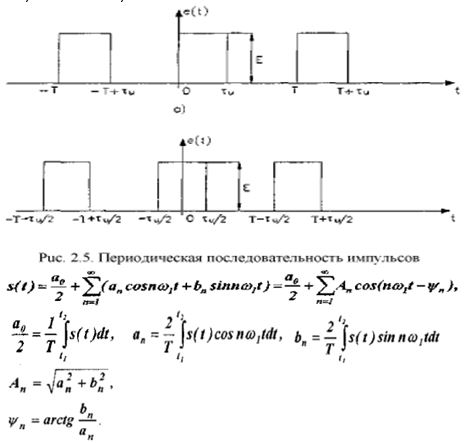
Для периодической последовательности импульсов (рис. 2.5а) с амплитудой Е и длительностью τ_µ. применяя формулы (2.4), (2.5) и (2.6). находим среднее значение (постоянную составляющую):

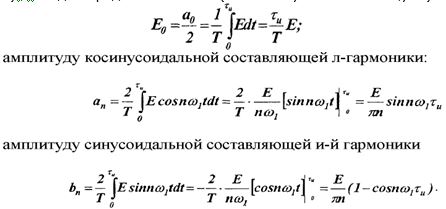
С помощью ф-л (2.7) и (2.8) находим амплитуду и фазу n-гармоники

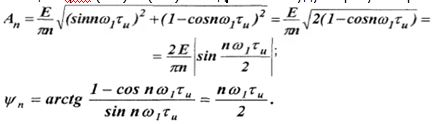
Подставляя в формулу, получим:

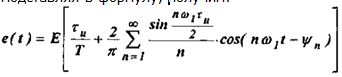
При другом выборе начала отсчёта времени функция e(t) является чётно относительно t:

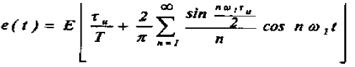
Отношение периода следования импульсов к амплитуде импульса называют скважностью: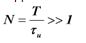 

Рассмотрим периодическую последовательность со скважностью 7

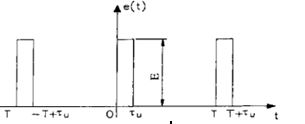
Спектр данной последовательности будет иметь вид:

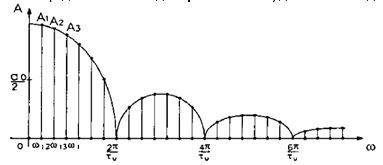
2)     Последовательность пилообразных импульсов.

Подобные функции часто встречаются на практике в устройствах для развёртки изображения на экране кинескопа:

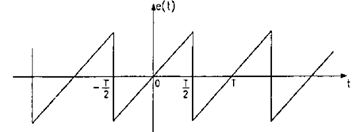
Так как эта функция является нечётной, ряд Фурье для неё будет содержать только синусоидальные члены:

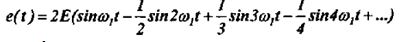
3)     Последовательность треугольных импульсов.

Сумма первых трёх членов этого ряда изображена на рисунке. Более быстрое убывание амплитуд гармоник объясняется отсутствием разрывов (скачков) в функции:

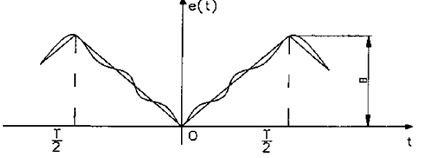
Ряд Фурье для этой функции будет иметь вид:

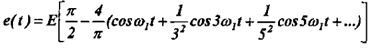
4)     Распределение мощности в спектре периодической последовательности импульсов.

Полная мощность периодической последовательности импульсов определяется суммой средних мощностей, выделяемых постоянной составляющей и гармониками.

Если гармонику представить током, то:

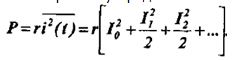
Черта над функцией означает усреднение значения функции от времени; r – сопротивление.

12Йі=PОЈP>   12PОЈ>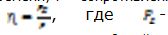 мощность ограниченного спектра;                            P- мощность колебаний.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.