Гауссовский случайный процесс. Одномерная плотность вероятности нормального распределения.

23.    Гауссовский случайный процесс

Нормальный (гауссовский) закон распределения случай­ных величин чаще других встречается в природе. Нормаль­ный процесс особенно характерен для помех в каналах связи. Он очень удобен для анализа. Поэтому случайные процессы, распределение которых не слишком отличается от нормального, часто заменяют гауссовским процессом. Одномерная плот­ность вероятности нормального процесса определяется выра­жением:

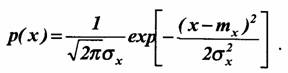
В данном случае будет рассматриваться стационарный и эргодический гауссовский процесс. Поэтому под т_х и σ _х можно подразумевать соответственно постоянную составляющую и среднюю мощность флуктуационной составляющей одной (до­статочно длительной) реализации случайного процесса.

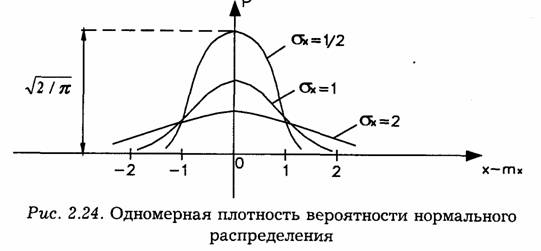
Графики плотности вероятности при нормальном законе для некоторых значений

σ _х изображены на рис. 2.24. Функ­ция р(х) симметрична относительно среднего значения. Чем больше σ _х, меньше максимум, а кривая становится более по­логой [площадь под кривой р(х) равна единице при любых значениях σ _х]

Широкое распространение нормального закона распреде­ления в природе объясняется тем, что при суммировании до­статочно большого числа независимых или слабо зависи­мых случайных величин распределение суммы близко к нор­мальному при любом распределении отдельных слагаемых.

Это положение, сформулированное в 1901 г. А. М. Ляпуно­вым, получило название центральной предельной теоремы. Наглядными физическими примерами случайного процес­са с нормальным законом распределения являются шумы, обусловленные тепловым движением свободных электронов в проводниках электрической цепи или дробовым эффектом в электронных приборах. Не только шумы и помехи, но и по­лезные сигналы, являющиеся суммой большого числа незави­симых случайных элементарных сигналов, например, гармо­нических колебаний со случайной фазой или амплитудой, ча­сто можно трактовать как гауссовские случайные процессы.

На основе функции р(х) можно найти относительное вре­мя пребывания сигнала x(t) в определенном интервале уров­ней, отношение максимальных значений к среднеквадратическому (пик фактора) и ряд других важных для практики параметров случайного сигнала.

Отношение времени пребывания x(t) в заданном интер­вале к общему времени наблюдения можно трактовать как вероятность попадания x(t) в указанный интервал. При этом следует заметить, что данные о распределении вероятностей не дают никаких представлений о поведении функции x(t) во времени.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.