Спектр периодической последовательности прямоугольных импульсов. Последовательность импульсов с большой скважностью. Спектр импульсной последовательности.

1)     Периодическая последовательность прямоугольных импульсов.

Рассмотрим спектры периодической последовательности прямоугольных импульсов.

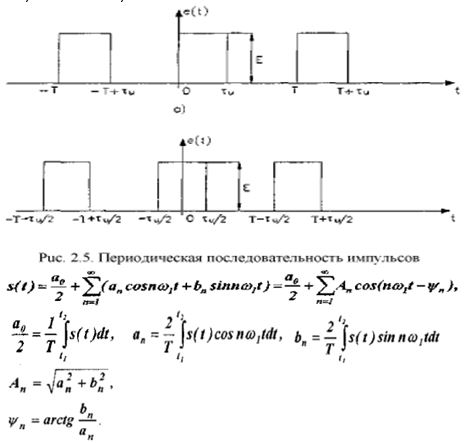
Для периодической последовательности импульсов (рис. 2.5а) с амплитудой Е и длительностью τ_µ. применяя формулы (2.4), (2.5) и (2.6). находим среднее значение (постоянную составляющую):

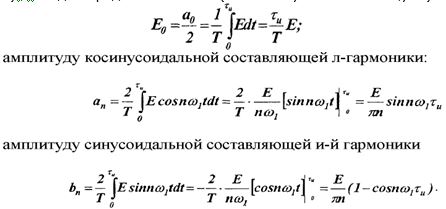
С помощью ф-л (2.7) и (2.8) находим амплитуду и фазу n-гармоники

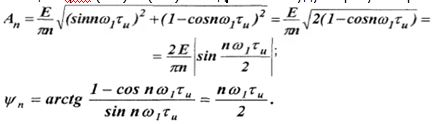
Подставляя в формулу, получим:

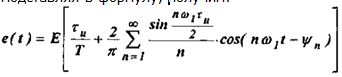
При другом выборе начала отсчёта времени функция e(t) является чётно относительно t:

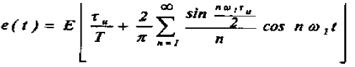
Отношение периода следования импульсов к амплитуде импульса называют скважностью: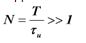 

Рассмотрим периодическую последовательность со скважностью 7

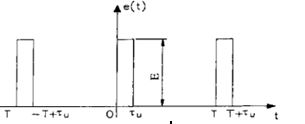
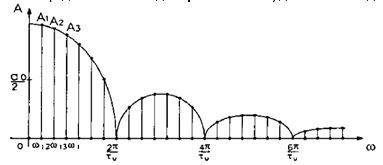
Спектр данной последовательности будет иметь вид:

2)     Последовательность пилообразных импульсов.

Подобные функции часто встречаются на практике в устройствах для развёртки изображения на экране кинескопа:

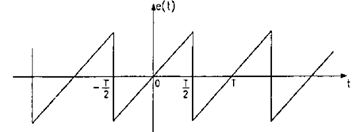
Так как эта функция является нечётной, ряд Фурье для неё будет содержать только синусоидальные члены:

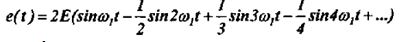
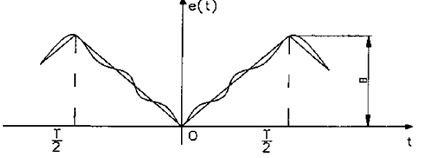
3)     Последовательность треугольных импульсов.

Сумма первых трёх членов этого ряда изображена на рисунке. Более быстрое убывание амплитуд гармоник объясняется отсутствием разрывов (скачков) в функции:

Ряд Фурье для этой функции будет иметь вид:

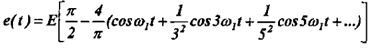
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.