Воздействие сигналов на нелинейные элементы. Примеркусочно-линейной аппроксимации. Нелинейный четырехполюсник иизбирательная цепь для выделения полезных составляющих спектра.

35. Воздействие сигналов на нелинейные элементы

`Основные преобразования сигналов осуществляются с помощью либо нелинейных электрических цепей, либо линей­ных цепей с переменными параметрами. Однако последние реализуются тоже с помощью нелинейных элементов (напри­мер, емкость p-n-перехода в полупроводниковом диоде).

Следует различать резистивные (сопротивления) и ре­активные (индуктивности, емкости) нелинейные элементы.

Наиболее характерными и распространенными резистивными нелинейными элементами являются полупроводниковые, ламповые и любые другие приборы, используемые для уси­ления или преобразования сигналов и имеющие нелинейную вольтамперную характеристику. Важным параметром резистивного нелинейного элемента является крутизна его харак­теристики. На рис. 3.11 приведены различные режимы рабо­ты нелинейного элемента.

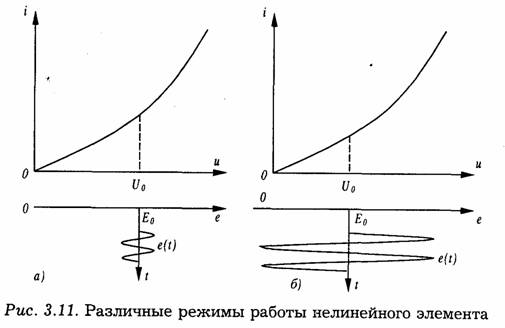
На рис. 3.11а в рассматриваемой рабочей точке U_o дей­ствует слабый сигнал e(t). Это соответствует линейному ре­жиму работы нелинейного элемента, который характеризует­ся дифференциальной крутизной:

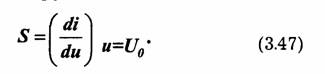
При воздействии сильного сигнала (рис. 3.116), что соответствует существенно нелинейному режиму работы элемен­та, вводится понятие средней крутизны. Средняя крутизна определяется с учетом формы вольтамперной характеристи­ки нелинейного элемента в широких пределах, зависящих от амплитуды входного сигнала.

Примером нелинейной емкости может служить любое ус­тройство с нелинейной вольткулонной характеристикой q(u) или вольтфарадной характеристикой с(и) = q(u)/u. В качестве нелинейной индуктивности L(i) может быть использована ка­тушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения.

Для анализа нелинейных цепей необходимо задать вольт-амперные или иные аналогичные характеристики нелиней­ных элементов в аналитической форме. Реальные характери­стики обычно имеют сложный вид, что затрудняет точное их описание с помощью достаточно простого аналитического вы­ражения.

Широкое распространение получили способы представ­ления характеристик относительно простыми функциями, лишь приближенно отображающими истинные характеристи­ки. Замена истинной характеристики приближенно представ­ляющей ее функцией называется аппроксимацией харак­теристики.

Оптимальный выбор способа аппроксимации зависит от вида нелинейной характеристики, а также от режима работы нелинейного элемента. Одним из наиболее распространенных способов является аппроксимация степенным полиномом.

Запишем аппроксимирующий степенной полином в форме:

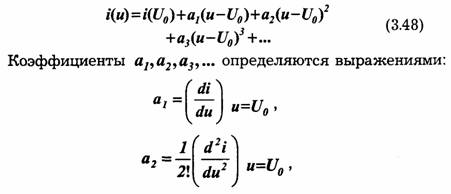
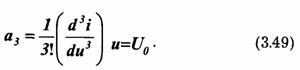
Нетрудно видеть, что а_; представляет собой крутизну ха­рактеристики в точке u = U₀, а₂ — первую производную кру­тизны (с коэффициентом 1/_2!), а₃ — вторую производную кру­тизны (с коэффициентом 1/_3!) и т. д. При заданной форме вольт-амперной характеристики коэффициенты a₁,a₂,a₃,... суще­ственно зависят от U₀, т. е. от положения рабочей точки на характеристике.

При очень больших амплитудах сигнала часто удобнее заменять реальную характеристику идеализированной, линей­но-ломаной, составленной из отрезков прямых линий. Такое представление характеристики называется кусочно-линейной аппроксимацией (см. рис. 3.12).

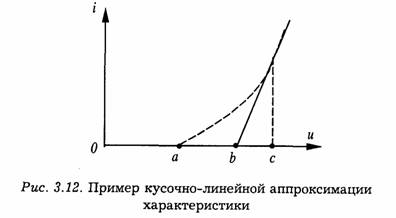
Следует особо подчеркнуть, что замена реальной нели­нейной характеристики линейными отрезками не означает ли­неаризации цепи. Например, несмотря на то, что на участке b-с (рис. 3.12) характеристика линейна по отношению к сигна­лу, захватывающему область изменения à-ñ, система в целом является существенно нелинейной.

Рассмотрим воздействие узкополосного радиосигнала на безынерционный нелинейный элемент. Под безынерционным нелинейным элементом подразумевается любой электронный прибор с нелинейной вольтамперной характеристикой при использовании его в диапазоне частот, на которых можно пре­небречь влиянием паразитных параметров (внутренних ем­костей и индуктивностей).

Рассмотрим режим работы, при котором вольтамперная характеристика i(u) удовлетворительно аппроксимируется степенным полиномом (3.48).

Сигнал e(t) зададим в форме гармонического колебания:

Выражения (3.51) — (3.54) полностью сохраняют свою структуру при замене постоянной начальной фазы 0_} моду­лированной фазой Ө₁ (t)=Ө_1max ∙ s(t). Из этого следует, что сфор­мулированные выше положения можно распространить так­же и на воздействие частотно-модулированного сигнала на резынерционный нелинейный элемент (при постоянной амп­литуде). Необходимо лишь каждую из гармоник тока с амп­литудой I_п трактовать как несущее колебание, модулирован­ное по углу. Это объясняется тем, что при угловой модуляции амплитуда колебания, несмотря на возникновение спектра боковых частот, остается неизменной.

Для первой (основной) гармоники индекс угловой моду­ляции совпадает с Ө_lmax =m₁, а для высших гармоник индекс пӨ_1тах=пт_1. Соответственно в n раз увеличивается и девиа­ция частоты.

Сказанное иллюстрируется рис. 3.13, где частота модуля­ции Ω<< ω₁. С увеличением номера гармоники ширина спек-тра боковых частот возрастает, но, как отмечалось выше, ам­плитуда суммарного колебания остается равной I_n.

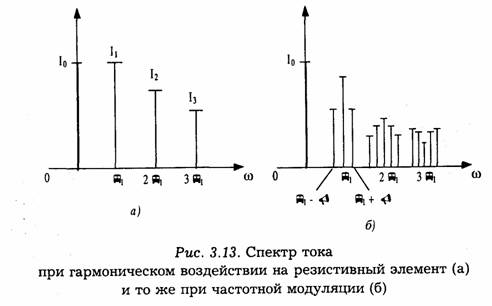
Для амплитудно-модулированного колебания, когда Е = E(t), нелинейность характеристики может коренным об­разом исказить форму передаваемого сигнала (нелинейное резонансное усиление, амплитудное ограничение и т. д.).

Рассмотрим воздействие суммы гармонических сигналов на нелинейный резистивный элемент.

Представим колебание в виде суммы:

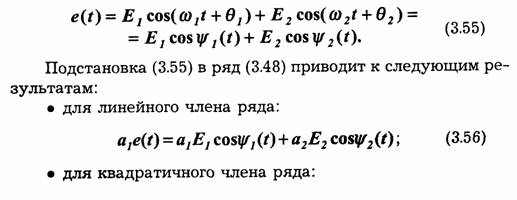
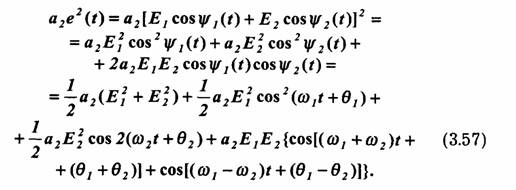
Первое слагаемое, не зависящее от времени, определяет приращение постоянного тока. Слагаемые с частотами 2ω₁ и 2ω₂ представляют собой вторые гармоники от соответствую­щих компонентов входного сигнала. Слагаемые же с частота­ми ω₁+ ω₂ и ω₁- ω ₂ представляют комбинационные колеба­ния.

Частоты, образуемые квадратичным слагаемым a₂e²(t), можно записать в форме:

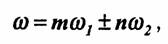
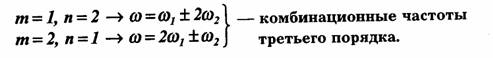
Приведенных выражений достаточно для установления закономерности образования частот гармоник и комбинаци­онных колебаний при воздействии двух гармонических состав­ляющих на нелинейный элемент:

•  слагаемые ряда (3.48) четной степени вносят в спектр тока гармоники и комбинационные частоты четных порядков;

•  слагаемые ряда (3.48) нечетной степени вносят в спектр тока гармоники и комбинационные частоты нечетных поряд­ков;

• число р = т + п определяет порядок колебаний, причем максимально возможный порядок р_тлх= k, где k — степень полинома, аппроксимирующего нелинейную характеристику.

Полученные результаты могут быть обобщены и на слу­чай воздействия суммы большого числа гармонических состав­ляющих на нелинейный элемент.

Содержание настоящего параграфа показывает, что не­линейная цепь преобразует спектр входного сигнала: возни­кают гармоники на кратных частотах и различные комбина­ционные колебания.

Принцип работы многих устройств преобразования сиг­налов основан на использовании тех или иных составляющих спектра тока на выходе безынерционного нелинейного эле­мента. Обобщенную структурную схему подобных устройств можно представить в виде сочетания нелинейной цепи и линейного фильтра (рис. 3.14).

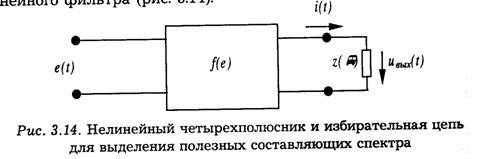
На рис. 3.14 изображена схема, соответствующая развя­занным нелинейному и линейному элементам, когда отсут­ствует обратная реакция выходного сигнала на ток в нели­нейной цепи. Нелинейная функция f(e), описывающая ха­рактеристику нелинейного элемента, зависит от его устрой­ства и от режима работы. Через z(ω) обозначено сопротивле­ние (комплексное) линейной частотно-избирательной цепи. Структура этой цепи, частотная характеристика и полоса про­пускания выбираются в зависимости от назначения устрой­ства.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.