B каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Код, исправляющий обнаруженные ошибки, называется исправляющим кодом. B этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Для того чтобы код обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.
Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определённому закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.
Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодахвсегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат исключительно для коррекции ошибок. В неразделимых кодах такое разделение провести невозможно.
Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.
В свою очередь, линейные коды могут быть разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Они характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю для любой пары комбинаций снова дает комбинацию, принадлежащую к этой группе.
В теории помехоустойчивого кодирования важным является вопрос об использовании избыточности для корректирования возникающих при передаче ошибок. Здесь удобно рассмотреть блочные коды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Для равномерных кодов число возможных комбинаций равно М= 2n, где n - значность кода.
В обычном некорректирующем коде без избыточности число комбинаций М выбирается равным числу сообщений алфавита источника Мо, и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число комбинаций источника M0. Однако в этом случае лишь М0 комбинаций из общего числа используются для передачи информации. Эти комбинации называются разрешёнными, а остальные М- М0 комбинации носят название запрещённых. Если переданная разрешённая комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях - исправлена. Естественно, что ошибки, приводящие к образованию другой разрешённой комбинации, не обнаруживаются.
Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние dy между двумя комбинациями Аi и Aj определяется количеством единиц в сумме этих комбинаций по модулю два. Например:
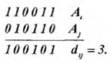
Для любого кода dy<=n. Минимальное различие между разрешенными комбинациями в данном коде называется кодовым расстоянием d. Ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации: g<=d-1. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d= 2.
Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешённой комбинацией и принятой запрещённой комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g-символов в n-значной комбинации будет равна:
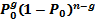
где P0- вероятность искажения одного символа. Так как обычно P0<< 1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещённая комбинация, то считается переданной ближайшая разрешённая комбинация. Это правило декодирования для распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального количества ошибок.