Логические основы построения вычислительной машины. Элементы алгебры логики. Логический синтез вычислительных схем.

Логические основы построения ВМ.

В вычислительных машинах коды нуля и единицы представляются электрическими сигналами, имеющими два различных состояния. Наиболее распространенными способами физического представления информации являются импульсный и потенциальный:

-импульс или его отсутствие;

-высокий или низкий потенциал;

-высокий потенциал или его отсутствие.

При импульсном способе отображения код единицы идентифицируется наличием электрического импульса, код нуля — его отсутствием (впрочем, может быть и наоборот). Импульс характеризуется амплитудой и длительностью, причем длительность должна быть меньше временного такта машины. При потенциальном способе отображения код единицы — это высокий уровень напряжения, а код нуля — отсутствие сигнала или низкий его уровень. Уровень напряжения не меняется в течение всего такта работы машины. Форма и амплитуда сигнала при этом во внимание не принимаются, а фиксируется лишь сам факт наличия или отсутствия потенциала. Вышесказанным обусловлено то, что для анализа и синтеза схем в компьютере
широко используется математический аппарат алгебры логики, оперирующий также двумя понятиями «истина» или «ложь». Алгебра логики применяется и при алгоритмизации и программировании решения задач

Элементы алгебры логики

Алгебра логики — это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: О и 1. Алгебра логики оперирует с логическими высказываниями.

Высказывание — это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, то есть каждое высказывание или истинно, или ложно, и не может быть одновременно и истинным и ложным.

Высказывания:

- «Сейчас идет снег» — это утверждение может быть истинным или ложным;

- «Вашингтон — столица США» — истинное утверждение;

- «Частное от деления 10 на 2 равно 3» — ложное утверждение.

В алгебре логики все высказывания обозначают буквами а, b, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем, если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры.

Простейшими операциями в алгебре логики являются операции логического сложения (иначе — операция ИЛИ (OR), операция дизъюнкции) и логического умножения (иначе — операция И (AND), операция конъюнкции). Для обозначения операции логического сложения используют символы + или V,а логического умножения — символы • или ^. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. В частности, для алгебры логики применимы законы:

1.Сочетательный:

2.Переместительный:

3.Распределительный:
Справедливы соотношения, в частности:

Также существует инверсия.

Логический синтез вычислительных схем.

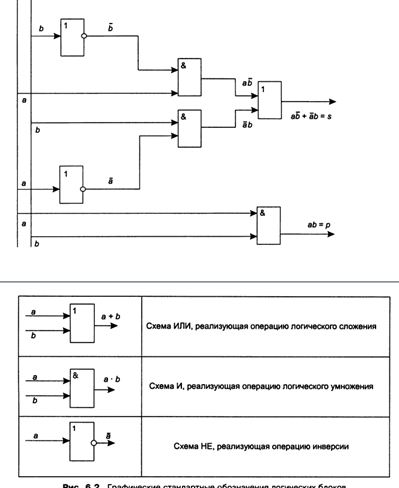
Рассмотрим логический синтез (создание) вычислительных схем на примере одноразрядного двоичного сумматора (полусумматора), имеющего два входа (а и Ь) и два выхода (5 и Р) и выполняющего операцию сложения.

Логическая блок-схема устройства, реализующего полученную функцию, представлена на рис. 6.1.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.