Скорость передачи информации и пропускная способность дискретных каналов с помехами.

34. Скорость передачи информации и пропускная способность дискретных каналов с помехами.

Воздействие помех па передаваемый сигнал приводит к разрушению и необратимой потере части информации, поступающей от источника сообщения. Поскольку в канале с помехами принятому сигналу υ_i может соответствовать передача одного из нескольких сигналов u, то после приема υ_i остается некоторая неопределенность в отношении переданного сигнала. Здесь соответствие между и и υ носит случайный характер, поэтому степень неопределённости характеризуется условной апостериорной вероятностью Р(u_i ; υ_i ), причем всегда P(u_i / υ_i) < 1 Количество информации, необходимое       для устранения оставшейся неопределённости

log (1/  P(u_i / υ_i )), очевидно, равно той части информации, которая разрушена вследствие действия помех. Тогда количество принятой информации определяется как разность:

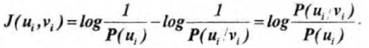 (1)

Величина J(u,v) характеризует в среднем количество информации, которое содержит принятый сигнал v относительно переданного сигнала и, поэтому ее называют средней взаимной информацией между и и v.

Выражение для  J(u,v)  обычно представляется в двух формах. Первая из них:

J(u,v)  = H(u)- H (u/ v),  (2)

где H(u)- энтропия источника сигналов u

     H (u/ v)- условная энтропия, или ненадежность

вторая: J(u,v)  = H(v)- H (v / u),

 где H(v) – энтропия выхода канала

       H (v / u) – условная энтропия, равная энтропии шума

Скорость передачи информации по каналу с помехами определяется как:

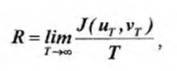
где и_Т и v_T - соответственно последовательности передаваемых и принимаемых сигналов длительностью T.

Необходимым условием применимости формулы  является соблюдение свойства эргодичности как для последовательностии_Т, так и последовательности v_T. Последнее означает, что помехи, действующие в канале, также должны быть эргодическими.

Выражение для скорости передачи можно представить в более удобных формах:

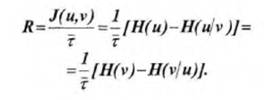
Пропускная способность канала с помехами определяется как максимально возможная скорость передачи при заданных ограничениях, накладываемых на передаваемые сигналы:

С = R_max

Для каналов с сигналами одинаковой длительности, равной, пропускная способность:

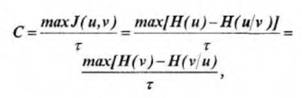  (3)

где максимум ищется по всем возможным ансамблям сигналов u.

Для многопозиционного симметричного канала при т_и=т_v = т>2:

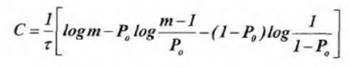
На рис. 6.2 приведена зависимость С от вероятности ошибки для двоичного канала

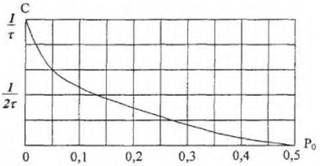
Увеличение вероятности ошибки Р_о приводит к снижению пропускной способности, которая становится равной нулю при Р_о=0,5. В этом случае полностью исчезает какая-либо зависимость между передаваемыми и принятыми сигналами:

Р(υ₁ / и₁)= P(v₂ /u₁ ) =1/2 и Р(υ₁ / и₂)= P(v₂ /u₂ ) =1/2  , значение Р_о = ¹/2 для бинарного канала является предельным.