Главная
»
Информационные системы
»
Архитектура ЭВМ
»
Выполнение арифметических операций в компьютере. Особенности выполнения операций над числами с плавающей запятой.
Выполнение арифметических операций в компьютере. Особенности выполнения операций над числами с плавающей запятой.
Выполнение арифметических операций в компьютере
Правила выполнения арифметических операций в двоичной системе счисления аналогичны правилам операций в десятичной системе счисления.
Например:
Сложение | 101110 | Вычитание | 101110 |
| 001011 | | 001011 |
Результат | 111001 | Результат | 100011 |
Умножение | 101101 | Деление | 101101 |
| х 101 | | /101 |
| 101101 | | 01 |
| 000000 | | 010 |
| 101101 | | 0101 |
Результат | 11100001 | Результат | 1001 |
(произведение) | | (частное) | |
Особенности выполнения операций над числами с плавающей запятой
При сложении (вычитании) чисел с одинаковыми порядками их мантиссы складываются (вычитаются), а результату присваивается порядок, общий для исходных чисел. Если порядки исходных чисел разные, то сначала эти порядки выравниваются (число с меньшим порядком приводится
к числу с большим порядком), затем выполняется операция сложения (вычитания) порядков. Если при выполнении операции сложения мантисс возникает переполнение, то сумма мантисс сдвигается вправо на один разряд, а порядок суммы увеличивается на 1.
При умножении чисел с плавающей запятой их мантиссы перемножаются, а порядки складываются.
При делении чисел с плавающей запятой мантисса делимого делится на мантиссу делителя, а для получения порядка частного из порядка делимого вычитается порядок делителя. При этом если мантисса делимого больше мантиссы делителя, то мантисса частного окажется больше 1 (происходит переполнение) и ее следует сдвинуть на один разряд вправо, одновременно увеличив на единицу порядок частного.
Выполнение арифметических операций в двоичной системе счисления.
Внутри компьютера арифметические операции в основном выполняются над двоичными числами. Для случая больших вычислений над десятичными числами, с целью повышения производительности, вместе с двоично-десятичным представлением в процессоре предусмотрено выполнение операций в двоично-десятичном режиме. Вычисления над числами с высокой точностью выполняется математическим сопроцессором в формате с плавающей запятой.
Рассмотрим порядок выполнения операций над двоичными целыми числами.
Сложение и вычитание.
В ЭВМ сложение и вычитание выполняется одной операцией над кодированными числами. При этом применяется насколько кодировок знака числа. Наиболее распространенным является дополнительный код.
Для представления положительного числа в дополнительном коде, нужно записать два знаковых нуля и дописать само число.
Пример: А=+1011, АдопМ=00’1011.
Чтобы снять кодировку положительного числа, два нуля заменяется знаком «+» и дописывается само число.
При представлении отрицательного числа, записываются две единицы указывающие что число отрицательное, а затем значения в разрядах числа инвертируются и к младшему разряду прибавляется единица.
Пример: А=-1011, АдопМ=11’0101.
Для снятия кодировки с отрицательного числа, две единицы заменяются на знак «-», значения в разрядах инвертируются, и к младшему разряду прибавляется единица.
При сложении и вычитании исходные числа выравниваются и представляются в дополнительном модифицированном коде. Затем выполняется поразрядное сложение (включая знаковые разряды). Если в знаковых разрядах появляется третий разряд равный единице, то он не учитывается и исключается из значения. Значения 10 и 01 в знаковых разрядах являются признаком того, что в результате операции произошло переполнение и полученное значение не верное. В этом случае в исходных числах в старших разрядах добавляются нули и операция повторяется.
Пример сложения чисел в дополнительном модифицированном коде:
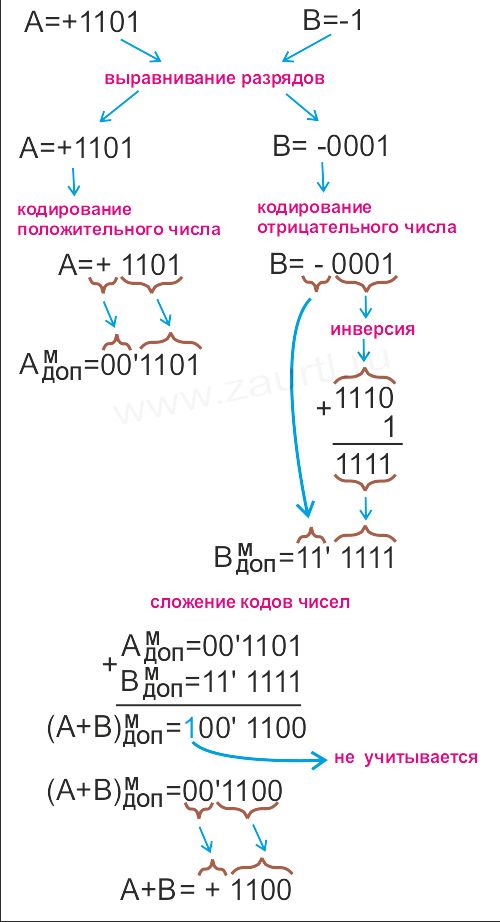
Пример сложения при переполнении разрядной сетки:
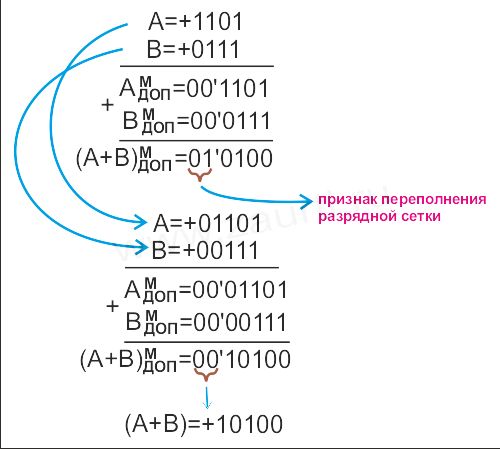
Умножение в двоичной системе счисления.
Операция умножения в двоичной системе выполняется довольно просто. Умножение заменяется на операции сдвига и сложения. Множимое записывается в столбик со сдвигом столько раз, сколько разрядов в множителе. В тех разрядах, где значение равно нулю соответствующая строка в столбике обнуляется. Затем все значения складываются.
Пример умножения чисел в двоичной системе счисления:
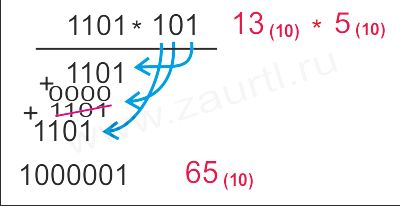
Деление в двоичной системе счисления.
Деление выполняется по тем же правилам что и в десятичной системе, но в двоичной системе действия выполняется особенно просто, так как очередная цифра частного может быть только нулем или единицей.
Пример деления чисел в двоичной системе счисления:
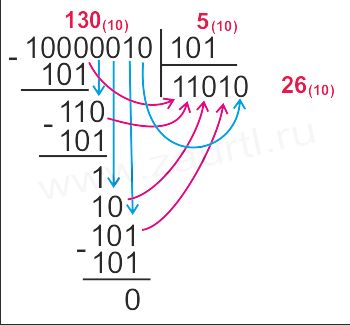
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.