Измерение информации по Шеннону.

Мера информации по Шеннону

В разделе 2.4 была приведена знаменитая формула Больцмана, определяющая связь энтропии со статистическим весом P системы

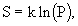 (1)

В середине XX века (1948 г.) была создана теория информации, с появлением которой введенная Больцманом функция (1) пережила второе рождение. Американский инженер-связист Клод Шеннон предложил ввести меру количества информации с помощью статистической формулы энтропии.

Заметим, что понятие информация обычно трактуется как сведения, а передача информации осуществляется с помощью связи. Связь между количеством информации и энтропией послужила ключом к решению ряда научных проблем.

Приведем ряд примеров. При бросании монеты выпадает орел или решка, это определенная информация о результатах бросания. При бросании кости получаем информацию о выпадении определенного количества очков (например, трех). В каком случае мы получаем больше информации?

Вероятность W выпадения герба равна 1/2, вероятность выпадения трех очков - W=1/6. Реализация менее вероятного события дает больше информации: чем больше неопределенность до получения сообщения о событии (бросание монеты, кости), тем большее количество информации поступает при получении сообщения. Информация I связана с числом равновероятных возможностей P - для монеты P=2, для кости P=6. При бросании двух костей получаем вдвое больше информации, чем при бросании одной кости: информация независимых сообщений аддитивна, а числа равновероятных возможностей перемножаются. Значит, если имеются два набора равновероятных событий P₁ и P₂ , то полное число событий

а количество информации I складывается, т. е.

Известно, что правилам (2) и (3) подчиняются логарифмические функции, т. е. зависимость количества информации I от числа равновероятных событий должна иметь вид

где постоянная А и основание логарифма могут быть выбраны по соглашению. В теории информации условились полагать А=1, а основание логарифма двум, т. е.

При бросании монеты получается информация (Р=2), которую примем за единицу информации I=1:

Бит - двоичная единица информации (binary digits), она оперирует двумя возможностями: да или нет, числа в двоичной системе записываются последовательностью нулей и единиц.

В общем виде (вывод) формула (4) принимает вид:

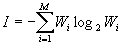 . (5)

Величина (5) названа Шенноном информационной энтропией.

Такой подход к количественному выражению информации далеко не универсален, т. к. принятые единицы не учитывают таких важных свойств информации, как ее ценность и смысл. Абстрагирование от конкретных свойств информации (смысл, ценность ее) о реальных объектах, как в дальнейшем выяснилось, позволило выявить общие закономерности информации. Предложенные Шенноном для измерения количества информации единицы (биты) пригодны для оценки любых сообщений (рождение сына, результаты спортивного матча и т. д.). В дальнейшем делались попытки найти такие меры количества информации, которые учитывали бы ее ценность и смысл. Однако тут же терялась универсальность: для разных процессов различны критерии ценности и смысла. Кроме того, определения смысла и ценности информации субъективны, а предложенная Шенноном мера информации объективна. Например, запах несет огромное количество информации для животного, но неуловим для человека. Ухо человека не воспринимает ультразвуковые сигналы, но они несут много сведений для дельфина и т. д. Поэтому предложенная Шенноном мера информации пригодна для исследования всех видов информационных процессов, независимо от вкусов потребителя информации.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.