Динамические сети.Самоорганизующиеся сети.

Динамические сети.

Они построены из динамических нейро­нов, чье поведение описывается дифференциальными или разностными уравнениями, как правило, первого порядка. Сеть организована так, что ка­ждый нейрон получает входную информацию от других нейронов (возмож­но, и от себя самого) и из окружающей среды. Этот тип сетей имеет важное значение, так как с его помощью можно моделировать нелинейные динами­ческие системы, например: ассоциативная па­мять, нелинейная обработка сигналов, моделирование конечных автоматов, идентификация систем, задачи управления.

СЕТИ ХОПФИЛДА

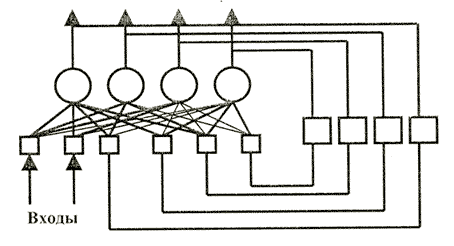
С помощью рекуррентных сетей Хопфилда можно обрабатывать неупо­рядоченные (рукописные буквы), упорядоченные во времени (временные ряды) или пространстве (графики, грамматики) образцы (рис. 13.4). Рекур­рентная нейронная сеть простейшего вида введена Хопфилдом; она построе­на из N нейронов, связанных каждый с каждым, причем все нейроны явля­ются выходными.

Сети такой конструкции используются, главным образом, в качестве ассо­циативной памяти, а также в задачах нелинейной фильтрации данных и грам­матического вывода. Кроме этого, недавно они были применены для предска­зывания и для распознавания закономерностей в поведении цен акций.

58.  Самоорганизующиеся сети.

Сеть такого типа рассчитана на самостоятельное обучение: во время обучения сообщать ей правильные от­веты необязательно. В процессе обучения на вход сети подаются различные образцы. Сеть улавливает особенности их структуры и разделяет образцы на кластеры, а уже полученная сеть относит каждый вновь поступающий при­мер к одному из кластеров, руководствуясь некоторым критерием «близости.

Сеть состоит из одного входного и одного выходного слоя. Количество элементов в выходном слое непосредственно определяет, сколько кластеров сеть может распознавать. Каждый из выходных элементов получает на вход весь входной вектор. Как и во всякой нейронной сети, каждой связи припи­сан некоторый синоптический вес. В большинстве случаев каждый выход­ной элемент соединен также со своими соседями. Эти внутренние связи иг­рают важную роль в процессе обучения, так как корректировка весов проис­ходит только в окрестности того элемента, который наилучшим образом от­кликается на очередной вход.

Выходные элементы соревнуются между собой за право вступить в действие и «получить урок». Выигрывает тот из них, чей вектор весов окажется ближе всех к входному вектору в смысле расстояния, определяе­мого, например, евклидовой метрикой. У элемента-победителя это рас­стояние будет меньше, чем у всех остальных. На текущем шаге обучения менять веса разрешается только элементу-победителю (и, может быть, его непосредственным соседям); веса остальных элементов при этом как бы заморожены. Выигравший элемент заменяет свой весовой вектор, немного перемещая его в сторону входного вектора. После обучения на достаточ­ном количестве примеров совокупность весовых векторов с большей точ­ностью приходит в соответствие со структурой входных примеров - век­торы весов в буквальном смысле моделируют распределение входных об­разцов.

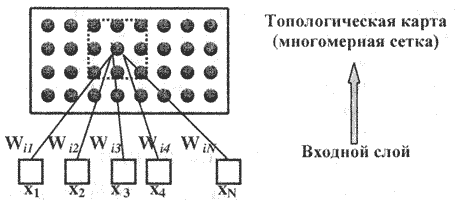
Самоорганизующаяся сеть Кохонена. Изображены только связи, идущие в i-u узел. Окрестность узла показана пунктиром

Очевидно, для правильного понимания сетью входного распределения нужно, чтобы каждый элемент сети становился победителем одинаковое число раз - весовые векторы должны бытьравновероятными.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.