Обработка свидетельств в условиях неуверенности и нечёткости. Меры неопределенности вИИС.

Обработка свидетельств в условиях неуверенности и нечёткости.

Истинное значение предложения зависит от уровня знания в то время, когда оно рассматривается.

Неопределенность и неточность данных могут рассматриваться как две противоположные точки зрения на одну и ту же реальность — непол­ноту информации. В этих условиях мы определим информационную еди­ницу четверкой (объект, свойство, значение, уверенность).

Неточность относится к содержанию информации, а неопределенность — к ее истин­ности, понимаемой в смысле соответствия действительности («уверенно­сти»). Степень неопределенности информации отражают с помощью квалификаторов (модальностей) типа «вероятно», «возможно», «необходимо», «правдоподобно» и др. Правдоподобность и доверие связаны с возможностью и необходимо­стью. Каждое из этих понятий соответствует некоторому способу вывода из заданной суммы знаний: заслуживает доверия все, что непосредственнодедуктивно выводится из базы знаний, а правдоподобно все, что не проти­воречит ей.

Информационное данное точное, если подмножество его значений является одиночным. Предложение неопределенное, если его справедливость или ложность не может быть определенноустановлена.

В нечеткой логике используются все значения между 0 и 1, чтобы указать частичную истину. Так, запись: Р(х) = 0,75 говорит о том, что предложение х в неко­тором смысле на три четверти истинно. Точно так же оно на одну четверть ложно.

Нечеткая реляционная база данных — это множество отношений, составленных из строк, содержащих n элементов.

Ответ на запрос есть отношение, образованное из области, релевантной запросу. В обычной базе данных каждая строка в отношении ответа полностью со­вместима с критерием выдачи, определенным в запросе. В нечеткой базе данных каждая строка получает некоторое значение функции принадлеж­ности. Обычно коэффициент степени принадлежности является мерой со­ответствия строки к данному размытому за­просу.

Ответ на размытый запрос будет иметь меру принадлежности, заключен­ной между нулем и единицей.

Меры неопределенности в ИИС.

Существуют две основных точки зрения на оценки вероятности, приме­няемые в экспертных системах: объективистский и субъективистский под­ходы. Согласно объективистскому подходу вероятность— это отношение появлений некоторого события к его наблюдениям в течение длительного периода времени. Другими словами, закон больших чисел гарантирует, что при наличии достаточных наблюдений процент появления событий будет приближаться к объективной вероятности.

Субъективистская или основанная на суждениях оценка вероятности исходит из того, что вероятностные меры уверенности представляют собою уверенность, которую индивидуум имеет относительно истинности некоторого конкретного предложения. Эта точка зрения постули­рует, что индивидуум действует некоторым «разумным» образом, что не исключает, однако, возможности того, что два разумно действующих инди­видуума, столкнувшись с одними и теми же данными, могут иметь разную степень уверенности в одном и том же высказывании.

Пусть А — событие в мире. Собрание всех возможных элементарных со­бытий Ω. называется пространством событий. Вероятность события А обо­значается р(А). Предположим, что В есть другое событие. Вероятность того, что А появится при условии, что В появилось, запишем в виде р(А/В). Р(А/В) называется условной вероятностью А при условии В:

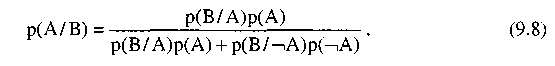
Равенство (9.8) закладывает основу для использования вероятности при оценке неопределенности.

В ИИС требуемые для решения проблемы вероятности обеспечиваются специалистами-экспертами и хранятся в базе данных. Эти вероятности включают априорные вероятности для всех возможных гипотез и ус­ловные вероятности для наблюдаемых порций свидетельств при условии гипотез.

Уверенность может накапливаться в ИИС системе в результате много­кратного использования правила Байеса для вычисления апостериорных ве­роятностей гипотез при условии наблюдаемых свидетельств. Полученные апостериорные вероятности обеспечивают ранжирование всех потенциально истинных гипотез.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.