Двумерные алгоритмы. Окна и Области вывода. Отсечение линий (общее представление, простой алгоритм). Автоматический подборразмеров и позиций.

2.Двумерные алгоритмы. Окна и Области вывода. Отсечение линий (общее представление, простой алгоритм). Автоматический подбор размеров и позиций.

ОКНА

Часто встречаются ситуации. Когда требуется вычертить объекты, размеры которых заданы в единицах, совершенно не совместимых с экранной системой координат.

Проблемно-ориентированные размеры выражаются в так называемых мировых координатах.(х,у).

Введем теперь понятие окна. Окно – это прямоугольник, в пределах которого вычерчивается объект (или его часть). Стороны прямоугольника параллельны координатным осям. Во избежание затруднений в понимании происходящего важно отметить. что окно относится к объекту, но не к изображению, которое будет сформировано. Очевидно, что размеры и положение окна определяется в системе мировых координат..

  Необходимо также задать прямоугольную область на экране, которая  определит размеры желаемой картинки. Эта область называется областью вывода. Она задается аналогично окну, то есть указываются минимальное и максимальное значения по координатным осям Х и У в единицах измерения на экране, значения которых будут определяться прописными буквами Х и У. Теперь окно нужно отобразить на область вывода. Вначале вычисляются коэффициенты масштабирования по осям:

              f_x=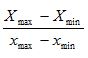 

               f_y=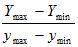

Затем расстояние X-X_min точки изображения от левого края области вывода вычисляется умножением коэффициента f_x  на соответствующее расстояние  х-х_min

От исходной точки до левого края окна. Расстояние Y – Y_min Следовательно, координаты точки изображения будут определены из соотношений

                  X = X_min + f_x (x  - x_min)

                   Y = Y_min + f_y (y – y_min)

Сделаем замечания.

1. Окно не обязательно должно охватывать весь объект.
2. f_x  и f_y  могут быть различны, но если углы на  изображении должны бытьтакими же как на объекте, то их надо установить равными, выбрав меньший из коэффициентов

ОТСЕЧЕНИЕ ЛИНИЙ

редположим, что мировые и экранные координаты одинаковые, то есть совпадают:

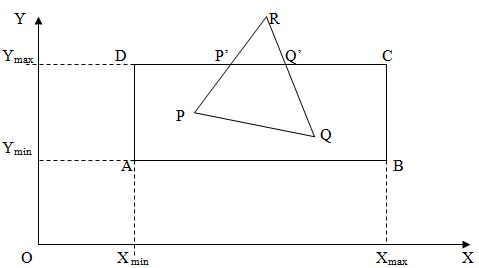
На рисунке показан прямоугольник ABCD, который является окном. В видимые отрезки и линии должны лежать внутри окна. То есть при вычерчивании отрезка прямой линии части, лежащие вне окна, должны быть отсечены. Процесс отсечения должен выполняться автоматически.

   На рисунке прямоугольник ABCD вычерчивается раньше, чем треугольник PQR, так что вместо этого треугольника надо вычертить ломаную PP’Q’Q.

   Поскольку заданы только три точки  P, Q и R, координатная пара (x_p’, y_p’) должна быть вычислена из значений координат точек (x_p, y_p)  и (x_R,y_R).Из рисунка видно, что наклон отрезка PR можно вычислить двумя способами,  что приводит к следующему уравнению

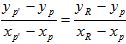
Совмещая это с соотношением

                              y_p = y_max

получим

x_p’ =  x_p +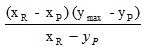 

Отсюда легко вычисляются координаты точки P’, если известно, что концевая точка Р находится внутри окна, а другая концевая точка R (x_R, y_R) удовлетворяет неравенствам

     x_min < x_R < x_max

     y_R > x_max

Однако необходимо рассмотреть значительно больше ситуаций. Представим их в таблице

 В этой таблице с любой точкой P (x, y) ассоциируется четырехбитовый код

b₃b₂b₁b₀, где b_i т быть либо 0, либо 1.

Запишем значения битов используя выражения языка Pasxal

b₃ = (x < x_min)

b₂ = (x > x_max)

b₁ = (y < y_min)

b₀ = (y > y_max)

АВТОМАТИЧЕСКИЙ ПОДБОР РАЗМЕРОВ И ПОЗИЦИЙ

Чтобы картинка была нарисована в пределах границ области вывода, необходимо сначала выполнить отсечение по заданному окну, а затем отразить окно и его содержимое на область вывода. Для многих приложений такая процедура вполне достаточна. Однако достаточно часто требуется другой подход, который отличается следующими аспектами:

1)      Объект будет вычерчиваться целиком, так что отсечение не понадобится;

2)      Окно будет определено расчетом, а не задано заранее;

3)      при отражении окна на область вывода будет использоваться одинаковый коэффициент масштабирования по обеим осям.

Из первого пункта следует, что объект должен быть конечным.

Пункт 2 может быть реализован путем двойного просмотра данных, описывающих объект. Во время первого просмотра определяются границы окна x_min, x_max, y_min, y_max,

Вычерчивание производится во время второго просмотра. Пункт 3 означает, что любой треугольник на картинке будет подобен исходному треугольнику на объекте, что означает неизменность угловых соотношений при отображении.

    В качестве коэффициента масштабирования  f выберем наименьшее из значений f_x, f_y:    f = min (f_x, f_y).

    Совершенно ясно, что такой одинаковый коэффициент масштабирования дет к отображению треугольника, который точно равен по величине размеру области вывода по одной из осей, а по другой может остаться свободное пространство. Таким образом изображение желательно поровну разделить соответственно между верней и нижней, между правой и левой частями области вывода. Для этого необходимо правильно рассчитать позицию центра С:

 x_c = (x_min + x_max) / 2

 y_c = (y_min + y_max) / 2

X_c = (X_min + X_max) / 2

Y_c  = (Y_min + Y_max) / 2

C_x = X_c – f x_c

C_y = Y_c – f y_c

 Для любой точки объекта (x, y)

   X = fx +c_x

Y = fy + c_y

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.