Двумерные алгоритмы Понятие о рекурсии. Понятие о фракталах. Сглаживание кривых

Рекурсия

В программировании рекурсия — вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Преимущество рекурсивного определения объекта заключается в том, что такое конечное определение теоретически способно описывать бесконечно большое число объектов. С помощью рекурсивной программы же возможно описать бесконечное вычисление, причём без явных повторений частей программы.

Реализация рекурсивных вызовов функций в практически применяемых языках и средах программирования, как правило, опирается на механизм стека вызовов — адрес возврата и локальные переменные функции записываются в стек, благодаря чему каждый следующий рекурсивный вызов этой функции пользуется своим набором локальных переменных и за счёт этого работает корректно. Оборотной стороной этого довольно простого по структуре механизма является то, что на каждый рекурсивный вызов требуется некоторое количество оперативной памяти компьютера, и при чрезмерно большой глубине рекурсии может наступить переполнение стека вызовов. Вследствие этого, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Впрочем, имеется специальный тип рекурсии, называемый «хвостовой рекурсией». Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного и/или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако, далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Любую рекурсивную функцию можно заменить циклом и стеком.

Данные

Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка (C++):

 class element_of_list

 {

   element_of_list *next; /* ссылка на следующий элемент того же типа */

   int data; /* некие данные */

 };

Рекурсивная структура данных зачастую обуславливает применение рекурсии для обработки этих данных.

Фрактал (лат. fractus — дробленый, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.

Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба.

Фрактал — самоподобное множество нецелой размерности.

Сжатие изображений

Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, см. Генератор фракталов (программа).

СГЛАЖИВАНИЕ КРИВЫХ

   В автоматизированном проектировании и управлении станками часто требуется построить гладкую кривую по набору заданных точек. Ограничимся пока анализом плоских кривых.

Из нескольких возможных способов построения гладких кривых выберем форму В-сплайна. Из заданной последовательности точек выбираются две соседние точки и между ними строится кривая кубического полинома на основе позиций четырех точек – двух уже упомянутых и двух соседних с ними точек. В-сплайн обеспечивает получение более гладких кривых, чем другие способы сглаживания за счет того, что получаемые кривые не проходят точно через заданные точки. Математическая гладкость кривых выражается в терминах непрерывности параметрических представлений  x(t) и y(t)  и их производных. К типа В-сплайна обладают свойством непрерывности даже вторых производных  x’’(t) и y’’(t) в точке стыковки двух соседних сегментов кривой. На рисунке показано, как выглядят кривые , если нулевая, первая или вторая производная не непрерывны в некоторой точке .

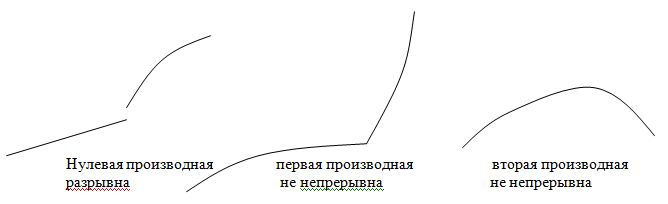
Последняя кривая может считаться гладкой, но она не удовлетворяет строгим требованиям, которые выполняются в способе В-сплайна.

  Рассмотрим этот метод в работе. Будем использовать параметрическое представление кривых. Любая точка части кривой между двумя заданными последовательными точками P и Q будет иметь координаты x(t) и y(t), где t увеличивается от 0 до 1, если отслеживается часть кривой от точки P до точки Q. Можно считать, что t – это время. Если имеются заданные точки

 P₀ (x₀, y₀)

P₁(x₁ y₁)

  ...

P_n(x_n y_n),

То часть кривой В-сплайна между двумя последовательными точками P_i  и P_i+1 получается путем вычисления значений функций x(t) и y(t) для изменения t  от 0 до 1

    x(t) = {(a₃t + a₂) t + a₁}t +a₀

     y(t) = {(b₃t + b₂) t + b₁}t +b₀

Эти уравнения содержат следующие коэффициенты:

a₃ = (- x_i-1 + 3 x_i – 3 x_i+1 + x_i+2)/6

a₂ = (x_i-1 – 2 x_i+ x_i+1)/2

a₁ = (- x_i-1 + x_i+1)/2

a₀ = (x_i-1 + 4 x_i + x_i+1)/ 6,

  а коэффициенты b₁, b₂, b₃, b₄ вычисляются по значениям y_i-1, y_i, y_i+1/ y_i+2 аналогичным образом..

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.