Главная » Информационные системы » Компьютерная геометрия и графика » 1.Двумерные алгоритмы. Преобразование координат: сдвиг, поворот.

1.Двумерные алгоритмы. Преобразование координат: сдвиг, поворот.

1.Двумерные алгоритмы. Преобразование координат: сдвиг, поворот.

Преобразование и новые координаты.

Рассмотрим следующую систему уравнений

\

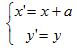
Эти уравнения можно интерпретировать двояким образом:

1. Все точки на плоскости ху переместились вправо на расстояние а
2. координатные оси х и у переместились влево на расстояние а

Этот простой пример иллюстрирует принцип, применимый и к более сложным ситуациям.  Мы  будем  рассматривать системы уравнений, обычно записываемых в виде произведения матриц, интерпретируя их как преобразование всех точек в фиксированной системе координат. Однако та же самая система может интерпретироваться и как изменение системы координат.

  Пусть необходимо повернуть точку Р(х,у) вокруг начала координат О на угол φ. Изображение новой точки обозначим P^’(x^’,y^’). Существуют четыре числа а,b,c,d, такие, что новые координаты х^’, y^’ могут быть вычислены по значениям старых координат х и у из следующих уравнений

x'=ax+by

y'=cx+dy

 Для получения значений а,b,c,d рассмотрим вначале точки (х, у) = (1, 0). Полагая х=1 и у=0 в этой системе получим

        x’=a

        y^’=c.

  Но в этом простом случае,как это видно из следующего рисунка, значения x^’ и y’ равны соответственно cos φ и sin φ. Тогда будем иметь

                а = cos φ

                с =  sin φ

Аналогичным образом из второй половинки рисунка следует

             b = - sin φ

             d  = cos φ

Тогда исходную систему можно переписать

          x’ = x cos φ – y sin φ

y

         y’ = x sin φ + y cos φ

 

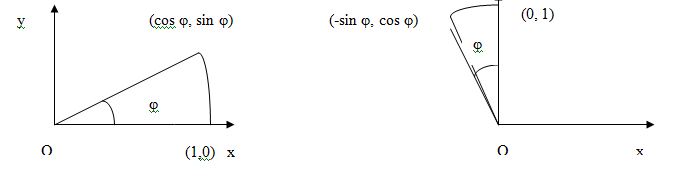
Поворот

Эта система описывает поворот вокруг начала координат, но обычно это не то, что требуется. Если требуется выполнить поворот относительно заданной точки  (х₀,у₀),то в этом уравнении можно заменить х на х-х₀, у на у-у₀, x’ на x’-x₀, y’ на у‘-у₀

  x' –x₀=(x-x₀) cos φ- (y-y₀) sin φ

  y' – y₀=(x-x₀) sin φ + (y-y₀) cos φ           (2)

 

Матричная запись

Система уравнений (2)  может быть записана в виде одного матричного уравнения

[x’ y’]= [x y]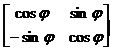 

 или с использованием вектора столбца

=

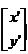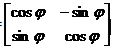
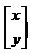
уравнение переноса можно записать в виде

 

[x’ y’] =[x y 1] 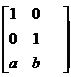, но лучше записать в виде

 

[x’ y’ 1] = [x y 1] .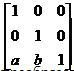

\

Запись каждого преобразования в форме произведения матриц позволяет совмещать несколько преобразований в одном. Чтобы показать такое совмещение  преобразований, объединим поворот с двумя переносами

  Поворот на угол φ вокруг начала координат запишем в форме

[x’ y’ 1] = [x y 1]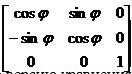

\

Выведем новую версию уравнения для описания поворота на угол φ вокруг точки (х₀ у₀). Это уравнение может быть выражено формулой

[x’ y’ 1] = [x y 1] R, где через R обозначена матрица 3 ^х 3.

Для нахождения этой матрицы R будем считать, что преобразование состоит из трех шагов с промежуточными точками (u₁ v₁), (u₂ v₂).

1. Преобразование переноса точки (х₀ у₀) в начало координат О. 

Т’ =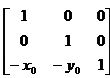 

\

2. Поворот на угол φ относительно начала координат О.

 [u₂ v₂ 1]=[u₁ v₁ 1] R₀, где

R₀ =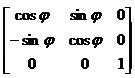 

\

3. Перенос из начала координат в точку (х₀ у₀)

 [x’ y’ 1] = [u₂ v₂ 1] T, где

T =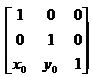 

\

Возможность комбинации этих шагов основано на свойстве ассоциативности матричного умножения

(А В) С = А (В С) или А В С

Теперь найдем

          [x’ y’ 1] = [u₂ v₂  1] T =

                        = ([u₁ v₁  1] R₀) T =

                        = [u₁ v₁  1] R₀ T =

                        = ([x y  1] T’)R₀ T =

                        = [x y  1] T’R₀ T =

                        = [x y 1] R

где

             R=T’ R₀ T

Это и будет искомая матрица, которая после выполнения матричного умножения даст

R =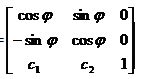

Где введены обозначения

                           c₁ = x₀  - x₀ cos φ + y₀ siun φ

                           c₂ = x₀ – x₀  sin φ –  y₀ cos φ .

 

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Поиск по сайту