Перенос и повороты в трехмерном пространстве.

Перенос и повороты в трехмерном пространстве.

   Если каждая точка P(x, y, z) отображается на точку  P’ (x’, y^’, z’) в соответствии с уравнениями

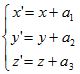
где а₁, а₂, а₃ – константы, то этот процесс называется переносом в трехмерном пространстве. Такой перенос может быть записан в матричной форме

[x’ y’ z’ 1] = [x y z 1] T

   T=

Поворот вокруг координатных осей может быть описан матрицей без использования однородных координат. Будем использовать правую координатную систему, считая вращение вокруг оси положительным, если оно соответствует положительному направлению этой оси по правилу винта с правой резьбой, как это показано на рисунке.

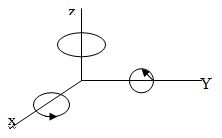
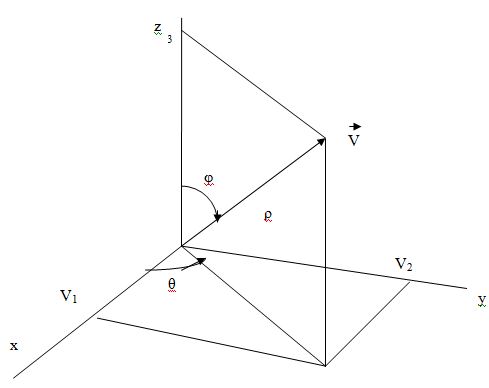
    Рассмотрим поворот вокруг  оси z  на угол  α и для сокращения обозначим cos α = c и   sin α = s. Тогда можно записать

[x’y’ z’]=[x y z] R_z

R_z =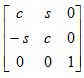 

\

Матрицу R_z можно использовать для получения матриц R_x  и R_y, определяющих поворот вокруг соответствующих осей, чисто формальным образом, то есть без применения картинки. Это делается путем циклических перестановок, получаемых заменой каждой из букв x, y, z на последующую, считая, что за буквой z следует буква х.

Матрица R_z превращается в матрицу R_x циклическим переносом каждой строки на одну позицию и затем выполнением аналогичной операции для столбцов:

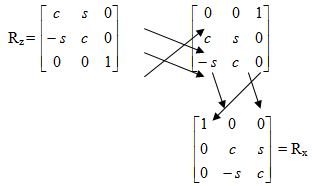
Так же матрица R_x преобразуется в «последующую» матрицу R_y

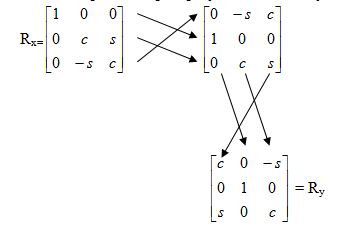
Суммируя сказанное, получим следующие матрицы

R_x=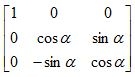                    

R_y=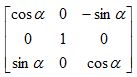 

R_z =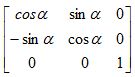       

\

Для поворота точки вокруг оси х на угол α матрица R_x используется следующим образом:

[x’ y’ z’] = [x y z] R_x

Матрицы R_y и R_z применяются аналогично.

Как известно, уравнения для преобразований могут интерпретироваться как изменения координат. Перенос точки на определенное расстояние вправо  описывает теми же уравнениями перенос системы координат на такое же расстояние влево. На практике удобнее перемещать координатную систему вместо точки, но для этого требуется инвертирование матрицы. Запишем для наших матриц соответствующие им инвертированные  матрицы.

Т^-1 =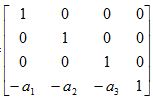

R_x^-1=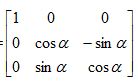

R_y^-1=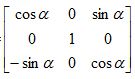

R_z^-1 =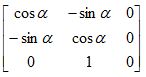

Теперь можно найти матрицу R для поворота вокруг любой прямой линии, проходящей через точку начала координат О. Для определенности будем полагать, что поворот осуществляется вокруг вектора v, начало которого расположено в точке О. Тогда положительное направление вращения соответствует направлению вектора по правилу винта с правой резьбой. Как и ранее поворот будем осуществлять на угол α.

   Если концевая точка вектора v задана в ортогональных координатах, то сначала вычислим его сферические координаты .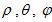

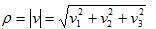
Если 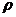= 0, то будем считать, что  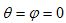. В противном случае

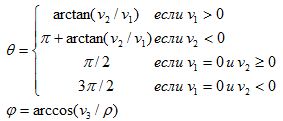
Возможно, Вы помните обратное вычисление

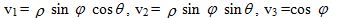
Теперь стратегия заключается в таком изменении системы координат, чтобы вектор v (ось вращения) совпадал с новым направлением  положительной полуоси z..

[x’ y’ z’] = [x y z] R_z^-1

R_z^-1 =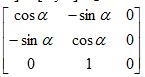

\

Ось x’ определяет положительное направление вектора (v₁, v₂, 0).

Теперь повернем оси x’ и z’ вокруг  оси y’ на угол 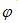 до совпадения оси z’ с вектором v.

Перепишем это условие как

[x’’ y’’ z’’]=[x’ y’ z’] R_y^-1

R_y^-1=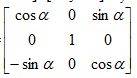

Фактический поворот вокруг вектора v на угол α теперь можно выполнить как поворот вокруг оси z’’ .То есть

[x’’’ y’’’ z’’’] =[x’’ y’’ z’’] R_v

R_v =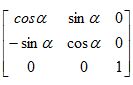     

К этому моменту достигнуто выполнение соотношения

[x’’’ y’’’ z’’’] =[x y z] R_z^-1 R_y^-1 R_v

Координаты [x’’’ y’’’ z’’’]  относятся к самой последней системе координат, тогда как их необходимо выразить в исходной системе. Обозначим эти координаты в исходной системе через x*, y*, z*. Переход к исходной системе инвертированных матриц R_z^-1  и R_y^-1 ,(которые будут совпадать с матрицами R_z и Ry) в обратном порядке для преобразования точки x’’’, y’’’, z’’’:

[x* y* z*] =[x’’’ y’’’ z’’’] R_y R_z

Это означает, что полный поворот вокруг вектора v на угол α вычисляется по формуле

[x* y* z*] =[x’’’ y’’’ z’’’] R_z^-1 R_y^-1 R_v R_y R_z

где

R_z^-1 =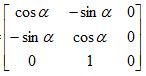

R_y^-1 =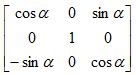 

R_v  =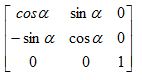        

R_y=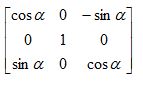 

R_z =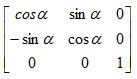       

Для последующего применения запишем

R_z^-1 R_y^-1 R_v R_y R_z =R =

До сих пор мы говорили о повороте относительно вектора, привязанного к точке начала координат – точке О. Теперь поставим задачу определения поворота относительно вектора, начало которого расположено в любой произвольной точке А (а₁, а₂, а₃). Для этого будем использовать вектор v для вычисления матрицы   R таким же образом, как и ранее. Затем нужно выполнить три следующих шага.

1.      Выполним перенос из заданной точки в точку начала координат О, используя однородные координаты и следующую матрицу:

         Т^-1=

2.  Осуществим поворот относительно оси, проходящей через точку О, как и ранее, но матрицу R обходимо тривиальным образом расширить, чтобы можно было использовать однородные координаты

R* =

3. Применим преобразование, обратное шагу 1, используя матрицу

T=

После этого матрица обобщенного поворота вычисляется как

              R_GEN = T^-1 R* T

И ее можно использовать следующим образом

[x* y* z* 1] = [x y z 1] R_GEN

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.