Однородные координаты.

Однородные координаты.

Сейчас нашей целью является более четкое понимание обозначений типа [x y 1] и       [x y z 1].

Мы уже использовали запись  [x y 1] для обозначения матрицы, состоящей только из одной строки, иногда называемой вектором-строкой. Такая запись может рассматриваться как частный случай записи [x y w], где числа  x, y, w называются однородными координатами. Эти три числа однородных координат применяются для обозначения точки в двумерном пространстве.

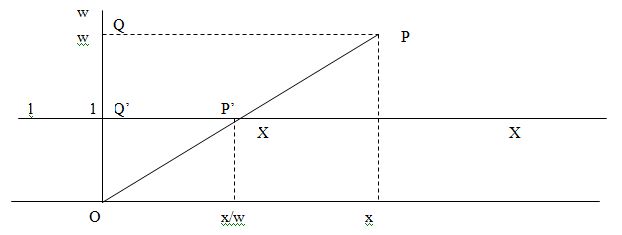
На рисунке имеем ось х и ось w, так что точка задается парой координат (x,w). Любая точка Р (x,y), не лежащая на оси х, имеет свою центральную проекцию Р’(X,1), определяемую как точка пересечения прямой линии ОР с прямой линией l, описываемой уравнением w=1.Точка начала координат является центром проекции. Отрезок прямой линии РО  может рассматриваться как луч света из объекта Р в глаз, расположенный в точке О. Для точек Q(0, w) и Q’(0,1) получим два подобных треугольника OPQ и OP’Q’, так что

                                                          X=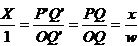

Все точки (x,w) со свойством x=wX лежат на линии ОР и имеют одну и ту же проекцию P’ Если интересоваться только проекциями на прямую линию l, а не фактическими значениями x и w, то имеет значение только их отношение. Вполне естественно учитывать только одну координату Х вместо пары (Х, 1), если учитывать только точки на прямой l. Если же все-таки требуется использовать координатную пару, то подойдет любая пара чисел (x,w), удовлетворяющая условию x/w=X. В геометрическом смысле координатная пара (wX, w) любой точки Р, отличной от О, на прямой ОР’ может служить обозначением точки P'. Это и реализуется в случае применения однородных координат.

  В общем случае любая точка (Х₁, Х₂, … , Х_n) в n-мерном пространстве записывается как точка (wX_1, wX₂, ...., wX_n, w) в n+1-мерном пространстве, где w – любое ненулевое вещественное число. Эта группа из n+1 чисел определяет однородные координаты исходной точки в n-мерном пространстве. Однородные координаты возникли из-за необходимости преобразования из n-мерного пространства в n+1-мерное. Точка (5,7) в двумерном пространстве, например, может быть записана в однородных координатах как (15, 21, 3) или (500, 300, 100). Хотя все операции относятся к двумерному пространству, эти точки можно принимать за точки в трехмерном пространстве. Очевидно, что обозначение  (X,Y) представляет собой обычную запись для точки (X, Y, 1)  в трехмерном пространстве. Точка P’ является центральной проекцией для любой точки P(x,y,w), если x/w=X и y/w=Y.

  Для определения термина однородные координаты воспользуемся уравнением aX+bY+c=0

Описывающим прямую в двумерном пространстве. Заменяя Х и Y на x/w и y/w, получаем

           a(x/w) + b(y/w) +c =0

или

            ax+by+cw=0.

  Последнее уравнение обычно принято называть однородным, поскольку оно имеет одинаковую структуру в терминах ax, by, cw.отсюда числа x, y, w закономерно называть однородными координатами точки (X, Y). Если принять, что двумерное пространство располагается на плоскости w=1 в координатной системе xyw, то это уравнение описывает плоскость, проходящую через начало координат и заданную прямую

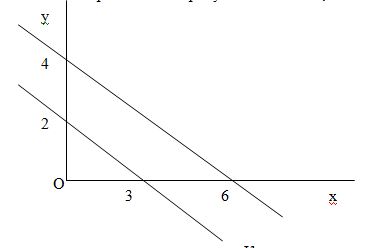
Система из двух линейных уравнений, каждое из которых описывает прямую линию в двумерном пространстве

\

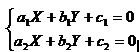
в случае, когда эти прямые параллельны, не имеет решения, то есть не существует пары чисел (X,Y), удовлетворяющей этой системе.

При замене координат X и Y на однородные координаты x, y, w мы получим систему

,

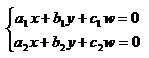уравнения которой можно интерпретировать как плоскости, проходящие через начало координат. Эта система имеет, по крайней мере, одно тривиальное решение x=y=w=0. Для геометрической интерпретации зададим для коэффициентов конкретные значения. Заменив, например,  предыдущую систему на систему

 ,

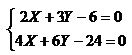описывающую две параллельные прямые. Заменим в ней координаты на однородные

\

Эта система эквивалентна системе

,

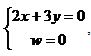Так что решение состоит из троек (3k, -2k, 0), где k –любое вещественное число. В трехмерном пространстве эти точки образуют прямую линию, проходящую через точки О и (3, 2, 0),причем  эта прямая представляет собой линию пересечения двух плоскостей, заданных уравнениями с однородными координатами.  Возвращаясь к двумерному пространству плоскости w=1, напомним, что каждая точка (X, Y) ассоциируется с прямой линией (wX, wY,  w) в трехмерном пространстве. Для ненулевых значений w эта ассоциация почти тривиальна. Теперь станет понятна очень важная причина применения однородных координат. Для каждой прямой линии в двумерном пространстве добавим один объект, называемый бесконечно удаленной точкой. Эта бесконечно удаленная точка не может быть обозначена в обычной системе а в однородной системе координат – может. Например, бесконечно удаленная точка на прямой линии, описываемой уравнением

,

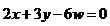записывается как (3, 2, 0) или в виде любой тройки (3k, 2k, 0) для ненулевого k. Поскольку эти тройки являются решением системы уравнений

,

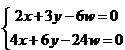то бесконечно удаленную точку можно считать точкой пересечения двух прямых, изображенных на рисунке. Считается, что бесконечно удаленная точка находится в

двумерном пространстве. Как мы видели, каждая точка в двумерном пространстве ассоциируется с прямой линией в трехмерном пространстве. Поэтому желательно выяснить, с какой прямой ассоциируется  бесконечно удаленная точка (3, -2, 0). Поскольку эта линия должна проходить через точку начала координат (0, 0, 0), то искомая линия должна  быть линией, проходящей через точку О и точку  (3, -2, 0), то есть лежащей в плоскости w=0.

  Вполне резонно назвать точку (3, -2, 0) бесконечно удаленной точкой, поскольку ее можно рассматривать как предельную точку (3, -2, w) при w, стремящемся к нулю, а эта тройка в однородных координатах эквивалентна  точке (3/w, -2/w, 1), которая при малых значениях w удалена очень далеко. Введение бесконечно удаленной точки позволяет утверждать,  что любые две различные прямые пересекаются в одной плоскости. Аналогично в проективной геометрии можно утверждать, что две любые различные плоскости имеют линию пересечения. Если плоскости параллельны, то все точки этой линии пересечения в однородных координатах записываются в виде

(x, y, z, 0). Этот вопрос мы не будем рассматривать детально, а вернемся к двумерному пространству и покажем новые возможности, предоставляемые однородными координатами.

  В обычных координатах линейное преобразование в двумерном пространстве может быть записано в виде

[X’ Y’] = [X Y] A

A=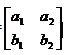

Поскольку [1 0] A = [a₁ a₂] и [0 1] A =[b₁ b₂], то строки матрицы отображают соответственно точки (1, 0) и (0, 1).

Вне зависимости от способа определения матрицы А начало координат О не изменяется, так как   [0 0]A = [0 0], поэтому этим способом нельзя выразить операцию переноса. Однако в однородных координатах точка в двумерном пространстве задается тройкой

(x, y, z) и преобразование записывается в виде [x’ y’ w’] = [x y w] A

A=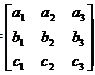

\

Мы имеем

 [1 0 0] A= [a₁ a₂ a₃]

Так как точка [1 0 0] бесконечно удаленная точка на оси х, то первая строка  [a₁ a₂ a₃] матрицы А представляет собой отображение этой бесконечно удаленной точки на оси х. Аналогично вторая строка матрицы [b₁ b₂ b₃] будет отображением бесконечно удаленной точки на оси y. Поскольку

[0 0 1] A = [c₁ c₂  c₃],

то можно считать, что третья строка матрицы [c₁ c₂  c₃] является отображением точки начала координат [0 0 1]. Это означает, что однородные координаты позволяют выразить любые преобразования путем матричного умножения.

Однако  операция переноса не единственное новое свойство,  предоставляемое таким матричным умножением. С его помощью можно преобразовать параллельные прямые в пересекающиеся. Покажем это на примере преобразования полного прямоугольного квадранта в треугольник.

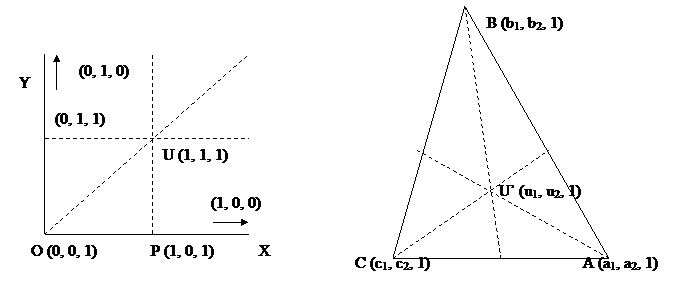
На рисунке изображен  произвольный треугольник, вершины которого заданы в прямоугольной системе координат точками А (а₁, а₂),  B (b₁, b₂), C (c₁, c₂). Добавим третью координату, равную 1, как формальное средство образования однородных координат. Исключением являются бесконечно удаленные точки (1, 0, 0) и (0, 1, 0) на координатных осях, у которых третья однородная координата равна нулю. Образуем матрицу М, такую, что матричное умножение

[x’ y’ z’] = [x y z] M

отобразит точку О на точку С, точку (1, 0, 0) на точку А и точку (0, 1, 0) - на точку В. Для любых ненулевых значений α, β, γ точки А, В и С будут точками  требуемого изображения треугольника если

М=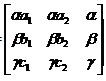

\

Это легко проверить, поскольку имеем очевидное соотношение

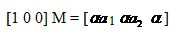
правая часть которого является просто другим обозначением точки А на рисунке. На первый взгляд кажется, что константы α, β, γ в нашем уравнении не нужны и могут быть установленными равными 1. Однако они нужны для того, чтобы можно было задать заранее установленное отображение U’ для так называемой единичной точки U. Точка U’ может быть выбрана в любом месте внутри треугольника. Поскольку точка U (1, 1, 1) отображается на точку U’ (u₁, u₂, u₃), то имеем

[1 1 1] M = [u₁ u₂ 1]

- сокращенное обозначение следующей системы трех линейных уравнений  относительно переменных α, β, γ:

a₁α + b₁β +c₁γ = u₁

a₂α + b₂β +c₂ γ =u₂

α + β + γ = 1

Система имеет единственное решение, которое следует из того факта, что тройки (а₁, а₂, а₃), (b₁, b₂, b₃) и (с₁, с₂, с₃) обозначают вершины треугольника. Решение этой системы для α, β, γ и подстановка результатов в уравнение

М=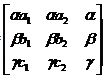           

\

Дает искомое значение матрицы М.

Прямые преобразуются в прямые, но их параллелизм не сохраняется.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.