Главная
»
Информационные системы
»
Компьютерная геометрия и графика
»
Методы устранения ступенчатости
Методы устранения ступенчатости
ОСНОВЫ МЕТОДОВ УСТРАНЕНИЯ СТУПЕНЧАТОСТИ
Чтобы эффективно бороться со ступенчатостью (лестничным эффектом), приводящей к искажениям в изображении, необходимо понимать причины, ее вызывающие. Основная причина появления лестничного эффекта заключается в том, что отрезки, ребра многоугольника, цветовые границы и т.д. имеют непрерывную природу, тогда как растровое устройство дискретно. Для представления отрезка, ребра многоугольника и т.д. на растровом устройстве необходимо начертить их в дискретных координатах, что может привести к удивительным результатам. Рассмотрим, например сигнал изображенный на следующем рисунке под буквой а. Второй сигнал более низкой частоты изображен на
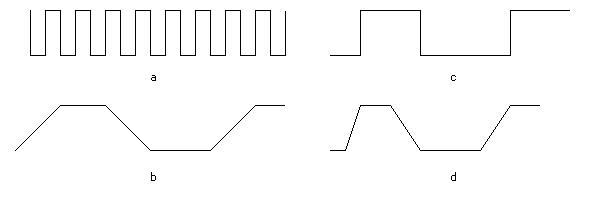
рисунке под буквой с. Если сделать выборки с одинаковой частотой из обоих сигналов, то восстановленные сигналы , показанные на рисунке под буквами с и d, идентичны. Рисунок d называется искажением выборки, показанной на рисунке под буквой b и, следовательно, сигнала на рисунке под буквой а. Для высокочастотного сигнала (рис. а) выборка проведена с недостаточной частотой. Для предотвращения искажения следует производить выборку сигнала с частотой по крайней мере вдвое превышающей частоту сигнала. Недостаточная выборка приводит к тому, что высокопериодичные изображения визуализируются неверно. Например, ограда забора или подъемные жалюзи могут выглядеть как несколько широких полос, а не как много отдельных, более узких полосок.
Рассуждения приведенные выше, и предыдущий материал иллюстрируют два из трех общих проявлений искажений такого рода в машинно-сгенерированных изображениях: ступенчатость ребер и некорректная визуализация тонких деталей или фактуры. Третье проявление связано с очень мелкими объектами. Если объект меньше размера пиксела или не покрывает внутреннюю точку, служащую для оценки атрибутов пиксела, то в данной ситуации весь пиксел будет иметь атрибуты маленького объекта. На правых пикселах следующего рисунка иллюстрируются объекты, которые будут проигнорированы или потеряны. Заметим, что могут быть проигнорированы также и длинные тонкие объекты. Особенно заметны такие эффекты в анимационных последовательностях кинокадров..
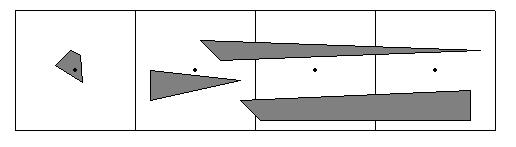
На следующем рисунке представлен маленький треугольник на трех кадрах анимационной последовательности. Если атрибуты пиксела определяются в его центре, то на первом кадре объект невидим, на втором видим, а на третьем снова невидим. В совокупности это будет выглядеть как мерцание объекта.
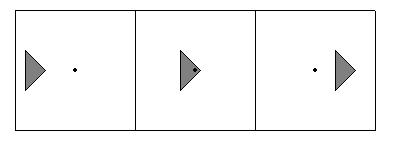
В основном существует два метода устранения искажений такого рода. Первый связан с увеличением частоты выборки, что достигается с помощью увеличения разрешения растра. Таким образом учитываются более мелкие детали. Однако существует определенное ограничение на способность растровых графических устройств с ЭЛТ выводить очень мелкие растры. Такое ограничение предполагает, что растр надо вычислять с более высоким разрешением, а изображать с более низким, используя усреднение некоторого типа для получения пиксела с более низким разрешением.
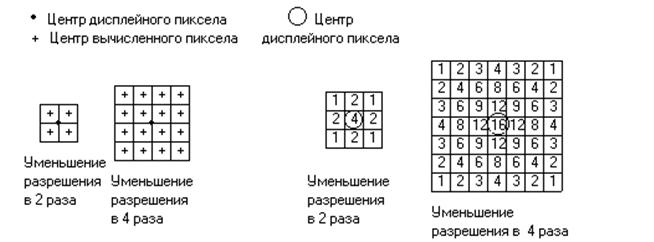
На рисунке показано усреднение двух типов. Равномерное усреднение окружающих пикселов для уменьшения разрешения в 2 и в 4 раза демонстрируется в левой части рисунка. Каждый дисплейный пиксел делится на подпикселы в процессе формирования растра более высокого разрешения. Для получения атрибутов дисплейного пиксела определяются атрибуты в центре каждого подпиксела, которые затем усредняются. В некоторой степени можно получить лучшие результаты, если рассматривать больше подпикселов и учитывать их влияние с помощью весов при определении атрибутов. В левой части рисунка представлены взвешенные средние для уменьшения разрешения в 2 и в 4 раза. Для этих взвешенных средних при уменьшении разрешения в 2 раза рассматриваются 9 пикселов, а при уменьшении в 4 раза – 49.
Второй метод устранения искажений изображений состоит в том, чтобы трактовать пиксел не как точку, а как конечную область.
Свертка и устранение ступенчатости
Распространение обсуждавшихся простых методов устранения ступенчатости (сглаживания) требует использование математического метода, называемого сверткой. Для сглаживания берется свертка сигнала, т. е. изображения, с ядром свертки. А результат используется для определения атрибутов пиксела. Свертка задается интегралом
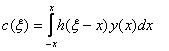
где
h(e, -x) – ядро или функция свертки,
у(х) – свертываемая функция,
с(e) – свертка h(x) и у(х)
Представить себе физический смысл свертки из ее математического определения весьма трудно. Однако нам в этом поможет простой графический анализ.
Рассмотрим свертку функции у(х) = х, 0х1 с простой прямоугольной функцией свертки h(x) = 1, 0<=x<=1. В графическом виде функция показана на следующем рисунке a.
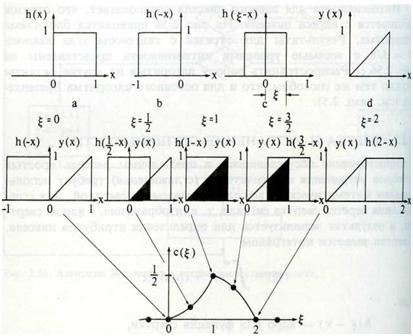
е= Эпселент!!!!
Для того чтобы получить h(-x), функцию надо отразить относительно ординаты (рис. b). Отраженное ядро для получения h(-x) переносится вправо на величину е (рис.с). Затем, как показано на рисунке ниже, ядро свертки и свертываемую функцию у(х) (рис. d) перемножают для разных значений величины. Площадь под объединенными кривыми (функциями) равна значению свертки с(е). Которая тоже изображена на рисунке с. Заметим, что в данном случае свертка не равна нулю только в диапазоне 0<=x<=2. Таким образом, определение свертки эквивалентно отражению ядра свертки, его сдвигу, перемножению двух функций и определению площади, заключенной под объединенными кривыми.
Математически ядро свертки равно
h(x) = 1 0<=x<=1
Отражение приводит к
h(-x) =1 -1<=x<=0
Перенос на эпселент дает
h(E, -x) =1 -1<=х<=E
Поскольку как ядро, так и свертываемая функция у(х) не равны нулю лишь на конечных интервалах, то пределы интегрирования в свертке тоже конечны. Как их определить. Из рисунка ясно, что нижний предел равен максимуму начал интервалов, на которых функции не равны нулю, а верхний предел равен минимуму концов этих интервалов. Таким образом,
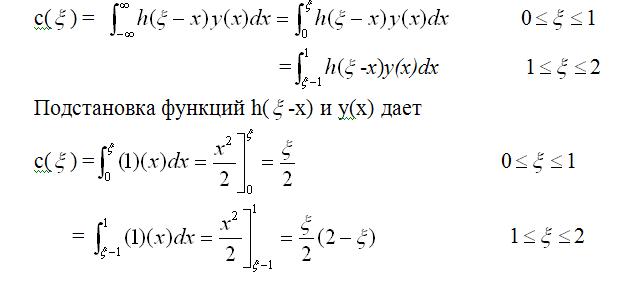
где обе функции параболические (нижняя часть рисунка). Если тангенс угла наклона равен m, а не 1, то результат можно обобщить в виде mE 2/2 и (m Е/2)(2-Е).
Чтобы понять, какая связь существует между сверткой и устранением ступенчатости (сглаживанием) вспомним эвристический метод модуляции интенсивности, в котором для определения интенсивности используется площадь пиксела. Проверка функции свертки c(Е) показывает, что для m<=1 значение свертки на правой стороне пиксела, т.е. при х=E= =1, равно площади той части пиксела, что находится внутри многоугольника, т.е. m/2 (рис б, с уi=0). Для m>1 значение свертки дает сумму площадей частей двух пересекаемых пикселов, расположенных внутри многоугольника (рис б, с уi=0). Этот результат легко обобщить на случай y(i)<>0. Таким образом, два предыдущих алгоритма (эский модулирования по площади и модифицированный Брезенхема) эквивалентны свертке функций ребер, т.е. прямой y = mx+ b и ядра свертки, вычисленных по правой стороне пиксела.
Операция свертки часто называется фильтрацией, а ядро свертки – функцией фильтра. В обсуждавшемся ранее простом методе с площадями изображение предварительно фильтруется. Префильтрация выравнивает атрибуты пикселов вычисленного разрешения с разрешением, большим, чем разрешение дисплея, и дальнейшее усреднение атрибутов нескольких пикселов для получения пикселов с меньшим разрешением можно рассматривать как постфильтрующую операцию.
Хотя при помощи простого прямоугольного фильтра или ядра свертки получают вполне приемлемые результаты, треугольный и гауссовский фильтр приводят к еще более качественным результатам. Используются также двумерные фильтры. В настоящее время исследованы простое прямоугольное, пирамидальное, конечное и двумерное гауссовские ядра свертки.
Простые фильтры в виде свертки не всегда эффективны для маленьких многоугольников с площадью, меньшей площади пиксела или для длинных тонких многоугольников. Тем не менее сглаживание можно реализовать с помощью отсечения. Стороны области пиксела образуют отсекающее окно. Каждый индивидуальный многоугольник отсекается по сторонам этого окна. Для модулирования интенсивности пиксела используется отношение площади полученного в результате отсечения многоугольника к площади пиксела. Если внутри пиксела находится несколько многоугольников, то используется среднее (либо равномерное, либо взвешенное) их атрибутов для модулирования пиксела.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.