Алгоритм определения невидимых линий.

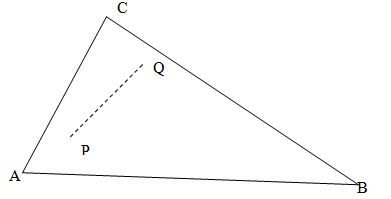
Рассмотрим теперь алгоритм, задача которого заключается в вычерчивании только видимых частей отрезка PQ.

Для каждого треугольника АВС из списка, записанного в массив Т, необходимо выполнить проверку – не будет ли он закрывать  PQ (или его часть). Как и ранее, Е – точка наблюдения. Будем говорить, что треугольник АВС закрывает точку R, если отрезок ER пересекает треугольник АВС в точке, внутренней как по отношению к отрезку, так и по отношению к треугольнику. Стороны треугольника не относятся к внутренним точкам,  а концевые точки отрезка не являются внутренними для отрезка. Таким образом, точка R не закрывается  треугольником АВС ни в том случае, когда точка R принадлежит внутренней части треугольника, ни в том случае, когда она принадлежит стороне треугольника, закрытой другим треугольником. Если треугольник АВС не закрывает точку R, то будем говорить, что точка R видима по отношению к треугольнику АВС. Если только конечное число точек отрезка PQ видимо по отношению к треугольнику АВС, все равно будем говорить, что АВС закрывает PQ. Если треугольник не закрывает PQ, нельзя сделать заключение, что все точки PQ видимы по отношению к этому треугольнику, поскольку треугольник может закрывать PQ частично. Треугольник АВС частично закрывает PQ, если он закрывает бесконечно много точек отрезка PQ и в то же время бесконечно много точек этого отрезка остаются видимыми по отношению к этому треугольнику.         

Если некоторый треугольник закрывает PQ, то нет необходимости учитывать оставшиеся треугольники в списке, но можно немедленно перейти к заключению, что PQ закрыт и не должен вычерчиваться.

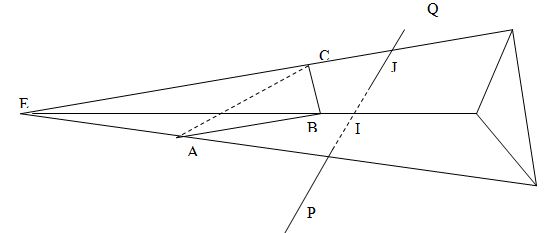Обсудим видимость отрезка PQ по отношению к треугольнику АВС в алгоритмическом смысле. Пусть заданы видовые координаты x_P, y_P, z_P, z_Q, ... для пяти точек P,Q, A, B, C и коэффициенты a,b,c,h уравнения ax+by+cz=h. Вся информация о треугольнике АВС сохраняется в элементе массива Т. Ключевым фактором в нашем анализе будет бесконечная пирамида, вершины которой находятся в точке Е, а боковые грани проходят через стороны треугольника АВ, ВС и СА. Эту пирамиду мы будем иметь ввиду употребляя слово «пирамида»,а треугольник АВС, употребляя слово «треугольник».

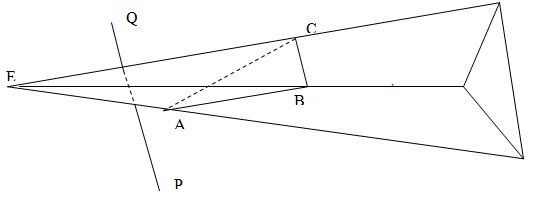
 Все точки внутри пирамиды позади треугольника будут невидимыми, а все точки впереди или вне пирамиды видимыми (относительно данного треугольника). На рисунке отрезок PQ пересекает пирамиду в двух точках I и J. Часть IJ отрезка PQ. Будет невидимой, а части PI и JQ видимыми.

Сложность задачи заключается в очень большом количестве случаев, которые предстоит рассмотреть. В ситуации, показанной на рисунке, можно вычислить положение точки I  Векторное представление прямой PQ записывается в виде

EP+λr,

где  r=[r₁ r2 r3] =PQ, откуда

           r₁= x_Q - x_P

                r₂ = y_Q -y_P

                r₃ = z_Q - z_P

точка (x,y,z) принадлежит прямой PQ, если

           x = x_P + λr₁

           y = y_P + λr_{2                          (*)}

           z = z_P + λr₃

для значений λ между 0 и 1 точка лежит между точками P и Q.Уравнение плоскости ЕАВ может быть записано как

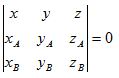
поскольку эта плоскость проходит через точки Е(0, 0, 0), А, В, уравнение можно переписать в виде

     C₁x + C₂y +C₃z = 0,

где

     C₁ = y_Az_B - y_Bz_A

      C_{2 =}  x_Bz_A - x_Az_{B     (**)}

      C₃ = x_Ay_B- x_By_A  

Подставляя правые части уравнения (*) в уравнение (**)  находим

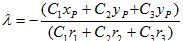
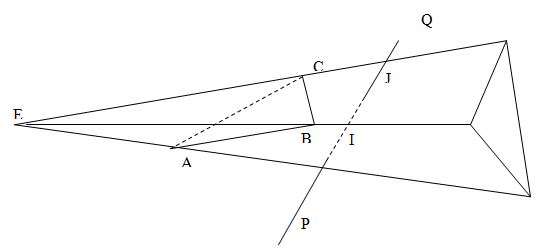
Используя значения λ в формуле (*), получаем координаты точки I. Изображенная на рисунке ситуация возникает только тогда, когда значение λ находится в пределах  от 0 до 1. Для других значений λ точка I лежит не на отрезке PQ, а на одном из его продолжений. Нельзя утверждать, что при значении λ от 0 до 1 отрезок PQ пересекает пирамиду, верно лишь обратное утверждение. На следующем рисунке показана ситуация, видимая из точки Е, когда значение  λ лежит в пределах от  0 до 1, хотя отрезок PQ не пересекает пирамиду.

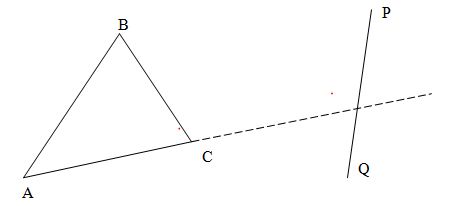
 Возвращаясь к трехмерному пространству (предыдущему рисунку), можно представить плоскость, проходящую через прямую линию PQ и точку наблюдения Е. Сейчас  мы хотим узнать, не будет ли эта плоскость проходить через точки, принадлежащие отрезку АВ. Для этого необходимо выполнить вычисления, аналогичные проводимым при определении значения λ. Запишем векторное представление прямой линии АВ

   ЕА + μАВ

точка (x,y,z) принадлежит прямой АВ, если

      x = x_A+μ(x_B-x_A)

      y = y_A +μ(y_B-y_A) (***)

      z = z_A + μ(z_B-z_A)

Для значений μ от 0 до 1 точка лежит между А и В.

Уравнение плоскости EPQ

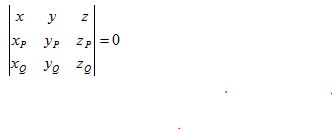
Перепишем это уравнение в виде

К₁х +К₂у +К₃z=0

где

K₁= y_P z_Q-y_Qz_P

K₂ = x_Qz_P-x_Pz_{Q  (****)}

K₃ = x_Py_Q- x_Qy_P

Совмещая (***) и (****) получаем

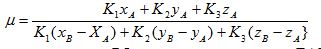
отрезок прямой PQ и плоскость пирамиды ЕАВ имеют общую точку, если, и только если

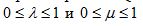
До сих пор мы рассматривали пересечение прямой PQ только с одной из плоскостей пирамиды, а именно с ЕАВ. Необходимо также рассмотреть плоскости ЕВС и ЕСА. Отрезок PQ может не иметь либо иметь одно или два пересечения с пирамидой. Соответственно, точки Р и Q могут лежать внутри, вне или на пирамиде, то есть располагаться впереди, позади или на плоскости АВС. Для проверки каждой пары из одного отрезка и одного треугольника может потребоваться большой объем работы. Обычно имеется очень много отрезков и каждый из них необходимо проверять относительно большого количества треугольников. Следовательно, такие проверки необходимо выполнять с большой эффективностью. Мы мм составить шесть тестов для проверки различных случаев, но желательно начинать с таких случаев, которые встречаются наиболее часто, и, если, тест, в этом случае закончился успешно, то остальные тесты можно (и нужно) игнорировать.

Тест 1.

 Если точки Р и Q лежат пред или на плоскости АВС (но не позади нее), то отрезок PQ – видимый. Это происходит когда

     ,

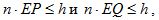где n=[a b c]. Напомним, коэффициенты a, b, c, h хранятся в массиве Т.

Этот тест охватывает и тот важный случай, когда PQ представляет собой одну из сторон треугольника.

Тест 2.

 Если прямая PQ лежит вне пирамиды, то линия PQ видима. Для выполнения теста можно подставить значения координат точек А, В, С в левую часть уравнения

,

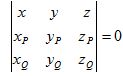определяющего плоскость ЕPQ. Если все три вычисления значения (для точек А, В и С) имеют одинаковые знаки (все положительные или все отрицательные), то все точки А, В и С лежат по одну сторону от плоскости EPQ. Следовательно, линия PQ расположена вне пирамиды и является видимой. Можно несколько ослабить это условие, допустив, что один из знаков равен нулю. Тогда, если обозначим каждый знак числами –1, 0 и 1 и будем проверять, не будет ли сумма знаков для точек А, В и С равна одному из чисел –3, -2, 2, 3. Заметим, что может произойти и такой случай, когда  точка Р совпадет с точкой А. Это важный специальный случай.

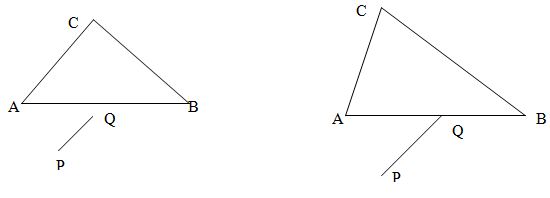
Тест 3.

Теперь найдем точку пересечения прямой PQ с плоскостями ЕАВ, ЕВС и ЕАС. Вычислим значения параметров λ для точки пересечения прямой PQ с плоскостью ЕАВ  по уравнению

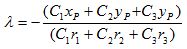
и μ по уравнению

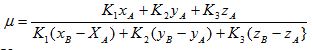
Уравнение

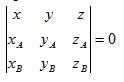
Описывает плоскость ЕАВ. Если левая часть этого уравнения при подстановке координат точек Р и С принимает разные знаки, то это означает, что точки Р и С лежат по разные стороны от прямой АВ. Если точка лежит за одной из сторон треугольника, то она расположена вне этого треугольника. Запомним эту информацию в логической переменной Ро. Аналогично для точки Q введем переменную Qo.Значения этих переменных будут проверяться в тестах 4 и 6. Если точки Р и Q лежат за одной и той же стороной треугольника или одна точка находится за стороной, а другая на стороне, то будем говорить, что отрезок PQ лежит вне этого треугольника. Тогда отрезок PQ – видимый. Важный специальный случай возникает при небольшой модификации рисунка, когда точка Q совпадает с точкой А. Заметим, что в отличие от рисунка к тесту 2, бесконечная прямая PQ в тесте 3 может пересекать отрезок ВС между точками В и С., так что тест 3 может быть выполнен и в том случае, когда тест 2 окажется невыполненным..

В большинстве случаев эта работа должна быть выполнена трижды: для каждой из плоскостей ЕАВ, ЕВС и ЕСА, следовательно, будет 3 пары значений (λ_i, μ_i) (i=1,2,3). Найдем минимальное и максимальное из значений λ_i, удовлетворяющих условиям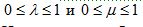     

И эти значения обозначим MIN и MAX, соответственно. Они являются побочным продуктом этого теста и определяются только тогда, когда он не выполнен.

Тест 4.

Если и точка Р, и точка Q находятся внутри пирамиды, а предыдущий тест не выполнен, то отрезок PQ лежит позади пирамиды и, следовательно, невидим. 

 При выполнении этого теста может встретиться весьма хитрая ситуация. Предположим, например, что отрезок PQ лежит на пирамиде позади отрезка АВ. Поскольку отрезок PQ не находится ни снаружи, ни внутри пирамиды, то кажется сомнительным, можно ли сказать, что треугольник закрывает отрезок PQ.Однако отрезок АВ может быть не ребром, а диагональю грани. Тогда эта грань определенно закрывает отрезок PQ и он не вычерчивается.  С другой стороны, если бы отрезок АВ был ребром объекта, то тогда отрезок PQ вычерчивать было бы не нужно, поскольку его изображение совпало бы с ребром АВ.

Тест 5.

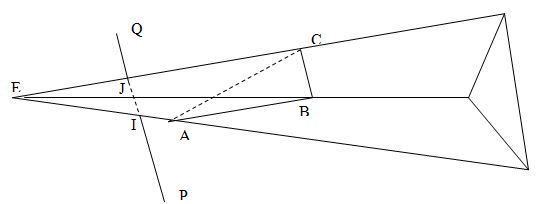
Если точка I, в которой прямая PQ пересекает пирамиду, лежит впереди треугольника, то прямая PQ видима. Это тест основан на том факте, что объект является сплошным телом, поэтому прямая PQ  может проходить через внутренние точки треугольника. Для нахождения такой точки I используем значения MIN и MAX параметра λ, вычисленные при выполнении теста 3. Затем можно проверить, не будет ли скалярное произведение векторов EI и n = [a b c] меньше, чем h.

Тест 6.

   Этот тест выполняется только в том случае, когда все предыдущие тесты не дали положительного результата, то есть когда прямая PQ пересекает пирамиду позади треугольника.

  Если значения MIN и MAX параметра λ указывают на точки пересечения I и J, как на рисунке ниже, тогда отрезок IJ будет невидимым и:

-          если точка Р находится вне пирамиды или перед плоскостью АВС, то отрезок PI видимый;

-          если точка Q находится вне пирамиды или перед плоскостью АВС, то отрезок QJ

-          видимый;

-          если точки P  и Q обе одновременно не находятся вне пирамиды, тогда точки I и J совпадают. Это показано на следующем рисунке

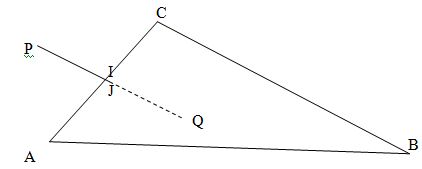
Во всех предыдущих случаях при определении видимости отрезка (по отношению к n-ому треугольнику) значение номера треугольника n увеличивается на 1. Затем проверяется отношение отрезка  PQ с остальными треугольниками, если они еще есть, или отрезок вычерчивается, если треугольников больше нет. Но в этом тесте могут появиться два новых отрезка PI и JQ, которые должны быть проверены с оставшимися треугольниками. Здесь можно будет рекурсивно дважды обратиться к этому же алгоритму. Для каждого рекурсивного обращения будем задавать концевые точки отрезка и номер треугольника, с которого должна начаться проверка.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.