Перспективное преобразование.

Здесь мировые координаты  уже не будут затрагиваться. Поэтому видовые координаты будут обозначаться просто (x, y, z) вместо (x_e, y_e, z_e).

На рисунке выбрана точка Q, видовые координаты которой равны (0, 0, d) для некоторого положительного числа d. Плоскость z=d определяет экран, который будем использовать.

 Таким образом, экран – это плоскость, проходящая через точку Q и перпендикулярная оси z.  Экранные координаты определяются  привязкой начала координат к точке Q, а оси

Х и Y имеют такие же направления, как оси х и у соответственно. Для каждой точки объекта Р точка изображения Р’ определяется как точка  пересечения прямой линии РЕ и экрана. Чтобы упростить рисунок, будем считать, что точка Р имеет нулевую у-координату. Но все последующие уравнения для вычисления ее у-координаты также пригодны и для  любых  значений координаты Х.

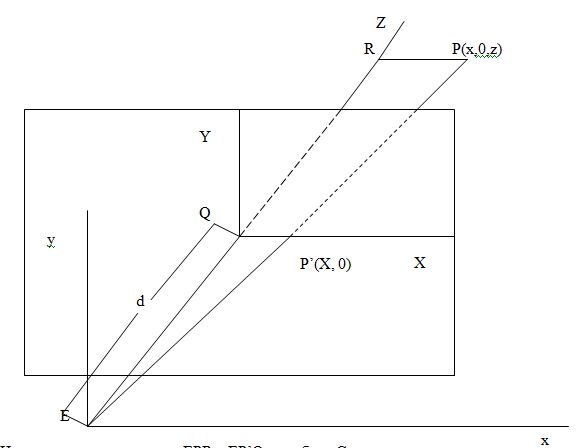
 На  рисунке треугольники EPR и EP’Q подобны. Следовательно,

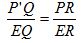
Отсюда будем иметь

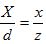
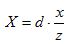
Аналогично можно получить

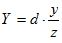
Ранее было введено предположение, что точка О начала системы мировых координат примерно совпадает с центром объекта. Поскольку ось z видовой системы координат совпадает с прямой ЕО, которая пересекает экран в точке Q, то начало Q системы экранных координат будет находиться в центре изображения. Если потребовать, чтобы это начало координат располагалось в нижнем левом углу экрана, а размеры экрана составляли 2с₁ по горизонтали и 2с₂ по вертикали, то наши последние уравнения можно заменить на следующие

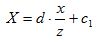
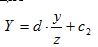
Нам еще требуется определить расстояние между точкой наблюдения Е и экраном. Грубо говоря, мы имеем соотношение:

,

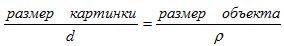что следует из подобия треугольников EP’Q’ и EPQ на следующем рисунке

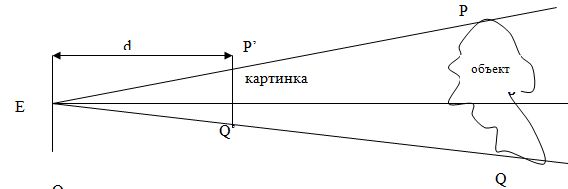
Отсюда получим

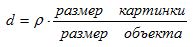
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.