Главная
»
Информационные системы
»
Компьютерная геометрия и графика
»
Построение реалистических изображений. Простая модель освещенности. Определение нормали к поверхности. Определение вектора отражения.
Построение реалистических изображений. Простая модель освещенности. Определение нормали к поверхности. Определение вектора отражения.
Построение реалистических изображений включает как физические, так и психологические процессы. Свет, т.е. электромагнитная энергия, после взаимодействия с окружающей средой попадает в глаз, где в результате физических и химических реакций вырабатываются электроимпульсы, воспринимаемые мозгом. Восприятие - это приобретаемое свойство. Психология зрительного восприятия широко изучалась, и о ней много написано, однако эта тема выходит за рамки данной книги. Проблемы зрительного восприятия хорошо описаны в книге [5-1].
Человеческий глаз - очень сложная система. Он имеет почти сферическую форму с диаметром около 20 мм. Воспринимаемый свет с помощью гибкого хрусталика фокусируется на сетчатке глаза, в которой есть два типа рецепторов: колбочки и палочки. В центре задней полусферы глаза собрано 6-7 млн. колбочек, чувствительных только к сравнительно высоким уровням освещенности, причем каждая из них присоединена к отдельному нерву. Колбочки позволяют различать мелкие детали. В сетчатке также находится 75-150 млн. палочек, чувствительных к очень низким уровням освещенности. К одному нерву присоединено сразу несколько палочек, поэтому они не способны различать мелкие детали. Интересно, что цвет воспринимается только колбочками, т. е. при низкой освещенности, когда колбочки теряют свою чувствительность, предметы кажутся черно-белыми.
Из опытов известно, что чувствительность глаза к яркости света изменяется по логарифмическому закону. Пределы чувствительности к яркости чрезвычайно широки, порядка 1010, однако глаз не в состоянии одновременно воспринять весь этот диапазон. Глаз реагирует на гораздо меньший диапазон значений относительно

a b
Рис. 5.1. Одновременный контраст.
яркости, распределенный вокруг уровня адаптации к освещенности. Чувствительность к относительной яркости имеет порядок 100-150 (2.2 логарифмической единицы). Скорость адаптации к яркости неодинакова для различных частей сетчатки, но тем не менее очень высока. Экстремумы диапазона относительной яркости воспринимаются соответственно как черный и белый.
Глаз приспосабливается к “средней” яркости обозреваемой сцены; поэтому область с постоянной яркостью (интенсивностью) на темном фоне кажется ярче или светлее, чем на светлом фоне. Это явление называется одновременным контрастом (рис. 5.1). Яркость центрального квадрата на шкале от 0 до 1 равна 0.5, а охватывающего - 0.2 (рис. 5.1, а). На рис. 5.1, b яркость центрального квадрата такая же, а охватывающего - 0.8. То же самое происходит при наблюдении уличного фонаря днем и ночью: если смотреть на фонарь днем (рис. 5.1, а), то средняя освещенность сцены выше, чем ночью (рис. 5.1, b). Поэтому уровень контраста ниже, и кажется, что интенсивность (яркость) фонаря или центрального квадрата на рис. 5.1, а меньше. Похожее на одновременный контраст явление существует и для цветов.
Еще одним свойством глаза, имеющим значение для машинной графики, является то, что границы областей постоянной интенсивности кажутся более яркими, в результате чего области с постоянной интенсивностью воспринимаются, как имеющие переменную интенсивность. Это явление называется эффектом полос Маха по имени открывшего его австрийского физика Эрнста Маха. Эффект полос Маха наблюдается, когда резко изменяется наклон кривой интенсивности. Если кривая интенсивности вогнута, то в этом месте поверхность кажется светлее, если выпукла - темнее (рис. 5.2).
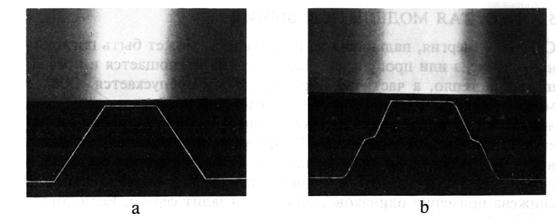
Рис. 5.2. Эффект полос Маха: (а) кусочно-линейная функция интенсивности, (b) функция интенсивности с непрерывной первой производной. (С разрешения университета штата Юта, [5-2].)
Эффект полос Маха особенно хорошо заметен на полутоновых поверхностях, заданных многоугольниками. Если интенсивность многоугольников определяется с учетом направления вектора нормали, то на ребрах этих многоугольников интенсивность будет резко меняться. Эффект полос Маха, мешающий глазу создавать сглаженное изображение сцены, виден на рис. 5.3, а. Увеличивая количество полигональных граней, его можно ослабить, но полностью уничтожить нельзя (рис. 5.3, b).

Рис. 5.3. Эффект полос Маха на поверхностях, образованных плоскими полигональными гранями: (а) модель с 8 гранями, (б) модель с 32 гранями. (С разрешения университета штата Юта, [5-2].)
5.2. ПРОСТАЯ МОДЕЛЬ ОСВЕЩЕНИЯ
Световая энергия, падающая на поверхность, может быть поглощена, отражена или пропущена. Частично она поглощается и превращается в тепло, а частично отражается или пропускается. Объект можно увидеть, только если он отражает или пропускает свет; если же объект поглощает весь падающий свет, то он невидим и называется абсолютно черным телом. Количество поглощенной, отраженной или пропущенной энергии зависит от длины волны света. При освещении белым светом, в котором интенсивность всех длин волн снижена примерно одинаково, объект выглядит серым. Если поглощается почти весь свет, то объект кажется черным, а если только небольшая его часть - белым. Если поглощаются лишь определенные длины волн, то у света, исходящего от объекта, изменяется распределение энергии и объект выглядит цветным. Цвет объекта определяется поглощаемыми длинами волн.
Свойства отраженного света зависят от строения, направления и формы источника света, от ориентации и свойств поверхности. Отраженный от объекта свет может также быть диффузным или зеркальным. Диффузное отражение света происходит, когда свет как бы проникает под поверхность объекта, поглощается, а затем вновь испускается. При этом положение наблюдателя не имеет значения, так как диффузно отраженный свет рассеивается равномерно по всем направлениям. Зеркальное отражение происходит от внешней поверхности объекта.
Свет точечного источника отражается от идеального рассеивателя по закону косинусов Ламберта: интенсивность отраженного света пропорциональна косинусу угла между направлением света и нормалью к поверхности, т. е.
I = Il kd cosq 0 £ q £ p /2
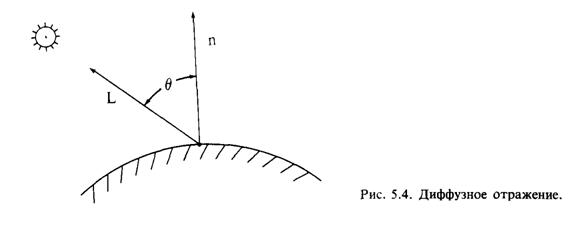
где I - интенсивность отраженного света, Il - интенсивность точечного источника, kd - коэффициент диффузного отражения (0 £ kd £ 1), q - угол между направлением света и нормалью к поверхности (рис. 5.4). Если q > p /2, то источник света расположен за объектом. Коэффициент диффузного отражения kd зависит от материала и длины волны света, но в простых моделях освещения обычно считается постоянным.
Поверхность предметов, изображенных при помощи простой модели освещения с ламбертовым диффузным отражением, выглядит блеклой и матовой. Предполагается, что источник точечный, поэтому объекты, на которые не падает
прямой свет, кажутся черными. Однако на объекты реальных сцен падает еще и рассеянный свет, отраженный от окружающей обстановки, например от стен комнаты. Рассеянному свету соответствует распределенный источник. Поскольку для расчета таких источников требуются большие вычислительные затраты, в машинной графике они заменяются на коэффициент рассеяния - константу, которая входит в формулу в линейной комбинации с членом Ламберта:
I = Iaka + Il kd cosq 0 £ q £ p /2 (5.1)
где Ia - интенсивность рассеянного света, ka - коэффициент диффузного отражения рассеянного света (0 £ ka £ 1).
Пусть даны два объекта, одинаково ориентированные относительно источника, но расположенные на разном расстоянии от него. Если найти их интенсивность по данной формуле, то она окажется одинаковой. Это значит, что, когда предметы перекрываются, их невозможно различить, хотя интенсивность света обратно пропорциональна квадрату расстояния от источника, и объект, лежащий дальше от него, должен быть темнее. Если предположить, что источник света находится в бесконечности, то диффузный член модели освещения обратится в нуль. В случае перспективного преобразования сцены в качестве коэффициента пропорциональности для диффузного члена можно взять расстояние d от центра проекции до объекта. Но если центр проекции лежит близко к объекту, то 1/d2 изменяется очень быстро, т. e. у объектов, лежащих примерно на одинаковом расстоянии от источника, разница интенсивностей чрезмерно велика. Как показывает опыт, большей реалистичности можно добиться при линейном затухании. В этом случае модель освещения выглядит так:
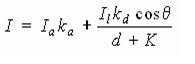
(5.2)
где K - произвольная постоянная.
Если предполагается, что точка наблюдения находится в бесконечности, то d определяется положением объекта, ближайшего к точке наблюдения. Это означает, что ближайший объект освещается с полной интенсивностью источника, а более далекие - с уменьшенной. Для цветных поверхностей модель освещения применяется к каждому из трех основных цветов.
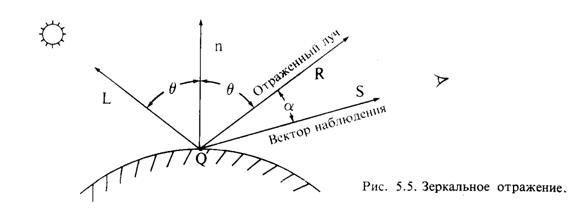
Интенсивность зеркально отраженного света зависит от угла падения, длины волны падающего света и свойств вещества. Основное уравнение Френеля приводится в любой книге по геометрической оптике. Зеркальное отражение света является направленным. Угол отражения от идеальной отражающей поверхности (зеркала) равен углу падения, в любом другом положении наблюдатель не видит зеркально отраженный свет. Это означает, что вектор наблюдения S (рис. 5.5) совпадает с вектором отражения R, и угол a равен нулю. Если поверхность не идеальна, то количество света, достигающее наблюдателя, зависит от пространственного распределения зеркального отраженного света. У гладких поверхностей распределение узкое или сфокусированное, у шероховатых - более широкое.
Благодаря зеркальному отражению на блестящих предметах появляются световые блики. Из-за того что зеркально отраженный свет сфокусирован вдоль вектора отражения, блики при движении наблюдателя тоже перемещаются. Более того, так как свет отражается от внешней поверхности (за исключением металлов и некоторых твердых красителей), то отраженный луч сохраняет свойства падающего. Например, при освещении блестящей синей поверхности белым светом возникают белые, а не синие блики.
В простых моделях освещения обычно пользуются эмпирической моделью Буи-Туонга Фонга [5-2], так как физические свойства зеркального отражения очень сложны. Модель Фонга имеет вид:
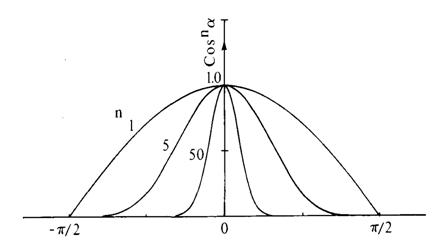
Рис. 5.6. Приближенные функции пространственного распределения для зеркального отражения.
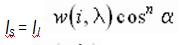 (5.3)
(5.3)
где w- кривая отражения, представляющая отношение зеркально отраженного света к падающему как функцию угла падения i и длины волны l ; n - степень, аппроксимирующая пространственное распределение зеркально отраженного света. На рис. 5.6 показана функция cos na при - p /2 £ a £ p /2 для различных n: большие значенияn дают сфокусированные пространственные распределения характеристик металлов и других блестящих поверхностей, а малые - более широкие распределения для неметаллических поверхностей, например бумаги.
Коэффициент зеркального отражения зависит от угла падения, однако даже при перпендикулярном падении зеркально отражается только часть света, а остальное либо поглощается, либо отражается диффузно. Эти соотношения определяются свойствами вещества и длиной волны. Коэффициент отражения для некоторых неметаллов может быть всего 4%, в то время как для металлических материалов - более 80%. На рис. 5.7, а коэффициенты отражения для типичных веществ при нормальном падении света показаны как функции длины волны, а на рис. 5.7, b - как функции угла падения. Обратите внимание, что при падении под скользящим углом (q = 90°) отражается весь падающий свет (коэффициент отражения 100%).
Объединяя эти результаты с формулой рассеянного света и диффузного отражения, получим модель освещения:
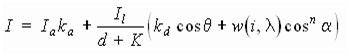 (5.4)
(5.4)
ОПРЕДЕЛЕНИЕ НОРМАЛИ К ПОВЕРХНОСТИ
Из предыдущего раздела видно, что нормаль к поверхности представляет ее локальную кривизну, а следовательно, и направление зеркального отражения. Если известно аналитическое описание поверхности, то нормаль вычисляется непосредственно. Но для многих поверхностей бывает задана лишь их полигональная аппроксимация. Зная уравнение плоскости каждой грани, можно найти направление внешней нормали (см. разд. 4.3).
Во многих алгоритмах удаления невидимых линий и поверхностей используются только ребра или вершины, поэтому, для того чтобы объединить их с моделью освещения, необходимо знать приближенное значение нормали на ребрах и в вершинах. Пусть заданы уравнения плоскостей полигональных граней, тогда нормаль к их общей вершине равна среднему значению нормалей ко всем многоугольникам, сходящимся в этой вершине. Например, на рис. 5.8 направление приближенной нормали в точке V1 есть
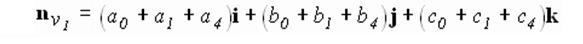
где а1....с4 - коэффициенты уравнений плоскостей трех многоугольников P0 , P1 , P4 , окружающих V1 . Отметим, что если требуется найти только направление нормали, то делить результат на количество граней необязательно.
Если же уравнения плоскостей не заданы, то нормаль к вершине можно определить, усредняя векторные произведения всех ребер, пересекающихся в вершине. Еще раз рассматривая вершину V1 на рис. 5.8, найдем направление приближенной нормали:
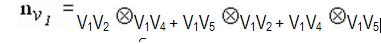
Следует обратить внимание на то, что необходимы только внешние нормали. Кроме того, если полученный вектор не нормируется, то его величина зависит от количества и площади конкретных многоугольников, а также от количества и длины конкретных ребер. Сильнее проявляется влияние многоугольников с большей площадью и более длинных ребер.
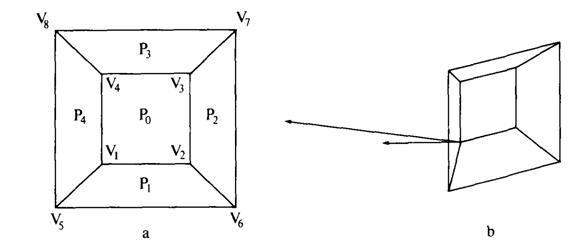
Рис. 5.8. Аппроксимация нормали к полигональной поверхности.
Когда нормаль к поверхности используется для определения интенсивности и для изображения объекта или сцены выполняется перспективное преобразование, то нормаль следует вычислять до перспективного деления [1-1]. В противном случае направление нормали будет искажено, а это приведет к тому, что интенсивность, задаваемая моделью освещения, будет определена неправильно.
ОПРЕДЕЛЕНИЕ ВЕКТОРА ОТРАЖЕНИЯ
Для модели освещения чрезвычайно важно правильно задавать направление векторов отражения. В примере 5.1 вектор отражения был найден из наблюдения. В данном разделе рассматриваются три наиболее общих метода. По закону отражения вектор падающего света, нормаль к поверхности и вектор отражения лежат в одной плоскости, причем на этой плоскости угол падения равен углу отражения (рис. 5.9, а). Фонг [5-2] вывел отсюда простое решение для случая, когда свет падает вдоль оси z. Это предположение удобно для модели освещения с одним точечным источником. Если начало системы координат перенести в точку поверхности, то проекции нормали и вектора отражения на плоскость хубудут лежать на одной прямой (рис. 5.9, b).
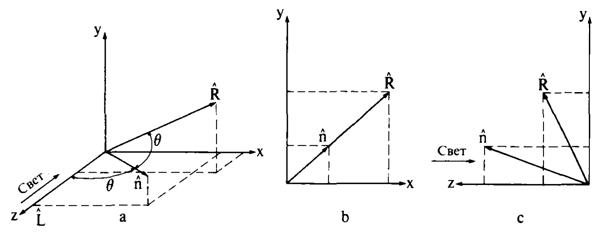
Рис. 5.9. Расчет направления отражения.
Таким образом,
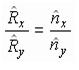
(5.8)
где Rx.....ny - суть x- и y-составляющие единичных векторов соответственно отражения и нормали.
Обозначим угол между единичным вектором нормали и осью z через q . Тогда составляющая вектора нормали по оси z есть

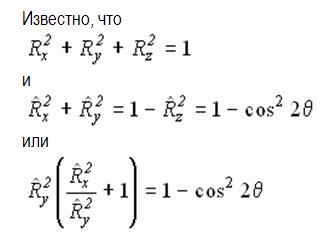
Используя отношение x- и y-составляющих векторов отражения и нормали (5.8) и соотношение
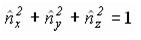
получаем
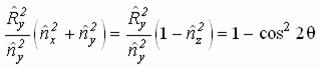
Перепишем правую часть:
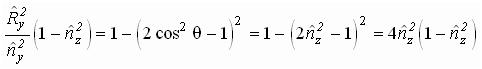
или
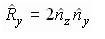 (5.10)
(5.10)
Из состояния (5.8) имеем
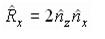
Когда свет падает не по оси я (например, когда источников несколько), таким методом воспользоваться нельзя. Можно перенести и повернуть каждый источник так, чтобы свет падал вдоль оси z, однако проще перенести и повернуть нормаль так, чтобы она была параллельна оси z, а точку Р поверхности принять за начало координат. Тогда плоскость хубудет касательной к поверхности, а х- и y-составляющие единичных векторов падения и отражения будут иметь разные знаки; z-составляющие этих векторов, будут, конечно, равны. Для того чтобы получить результаты в первоначальной ориентации, надо выполнить обратное преобразование. В перемещенной и повернутой системе координат
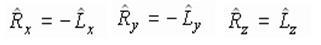
Этот метод особенно удобен, когда преобразования реализованы аппаратно или микропрограммно.
В третьем методе условие того, что единичная нормаль, единичный вектор падения и единичный вектор отражения лежат в одной плоскости, записывается при помощи их векторных произведений. Равенство углов падения и отражения выражается через скалярные произведения этих векторов. Из данных условий получаем
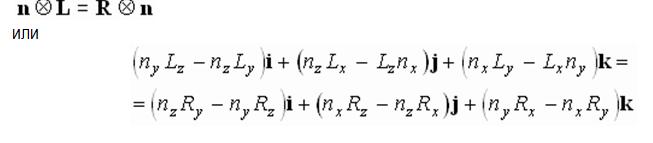
Векторные произведения совпадают, если равны их х-, у- и z-составляющие
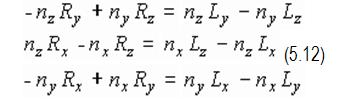
На первый взгляд может показаться, что вектор отражения найден. К сожалению, одно из этих уравнений всегда является линейно зависимым.
Запишем равенство углов падения и отражения: L*n=n*R
или
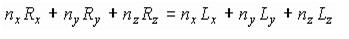 (5.13)
(5.13)
что дает необходимое добавочное условие. Матричный вид для всех уравнений с тремя неизвестными Rx Ry Rz таков:
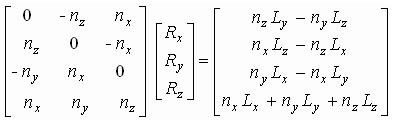
или
[N][R]=[B]
Поскольку матрица [N] не является квадратной, для решения системы нужны особые методы1). В частности,
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.