Видовое преобразование.

Для выполнения видовых преобразований должны быть заданы точка наблюдения, совпадающая с глазом и объект. Желательно, чтобы система мировых координат была правой. Будет удобно, если начало ее координат располагается где-то вблизи центра объекта, поскольку объект наблюдается в направлении от Е к О. Предположим, что это условие выполняется. На практике это означает, что возможно потребуется некоторое преобразование координат, заключающиеся в вычитании из исходных значений координат положения центральных точек объекта. Это очень простое преобразование будет включено в программу, но без записи в математической форме. Пусть точка наблюдения Е будет задана в сферических координатах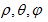 по отношению к мировым координатам. То есть мировые координаты могут быть вычислены по формулам:

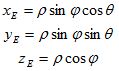
Обозначения сферических координат изображены на рисунке

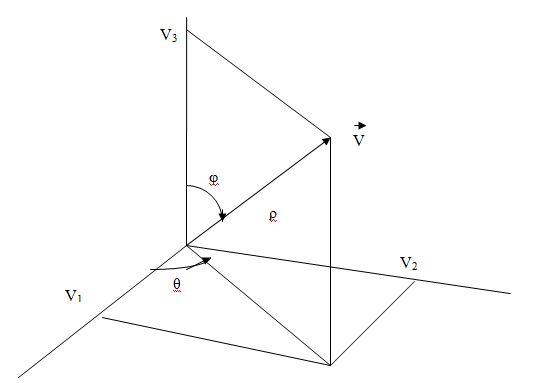
Говорят, что вектор направления ЕО (равный –ОЕ) определяет направление наблюдения. Из точки наблюдения  Е можно видеть точки объекта только внутри некоторого конуса, ось которого совпадает с линией ЕО, а вершина – с точкой Е. Если заданы ортогональные координаты 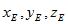 точки Е, то можно вычислить ее сферические координаты по методике, которую мы рассматривали. Нашей конечной задачей будет вычисление экранных координат Х, Y, для которых оси Х и Y лежат в плоскости экрана расположенного между точками Е и О и перпендикулярной направлению наблюдения ЕО.

Начало системы видовых координат располагается в точке наблюдения Е (см. рис.).

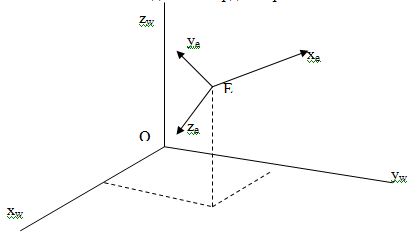
При направлении взгляда из Е в О положительная полуось х_е направлена вправо, а положительная полуось у_е – вверх. Такое направление осей позволит нам впоследствии определить экранные оси в тех же направлениях. Направление оси z_е выбирается таким образом, что значения координат увеличиваются по мере удаления от точки наблюдения. Такое определение осей логично и удобно, но их взаимное соответствие такого, что система видовых координат является левосторонней.

 Преобразование может быть записано в форме

,

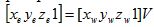где матрица V – матрица видового преобразования размером 4x4.  Для нахождения матрицы V предположим, что преобразования отображения могут быть составлены из четырех элементарных преобразований, для которых легко написать свои матрицы преобразований. Матрица V получается путем перемножения этих четырех матриц. Фактически каждое из четырех преобразований изменяет координаты и, следовательно, определяется матрицей, обратной матрице, соответствующей преобразованию точки.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.