Алгоритмы заполнения многоугольников

Генерацию сплошных областей из простых описаний ребер или вершин будем называть растровой разверткой сплошных областей, заполнением многоугольников или заполнением контуров. Для этого можно использовать несколько методов, которые обычно делятся на две категории: растровая развертка и затравочное заполнение.

  В методах растровой развертки пытаются определить в порядке сканирования строк, лежит ли точка внутри многоугольника или контура. Эти алгоритмы обычно идут от «верха» многоугольника или контура к «низу». Методы развертки также применимы и к векторным дисплеям, в которых они используются для штриховки или закраски контуров, как показано на рисунке.

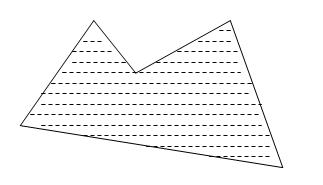
В методах затравочного заполнения предполагается, что известна некоторая точка (затравка) внутри замкнутого контура. В алгоритмах ищут точки, соседние с затравочной и расположенные внутри контура. Если соседняя точка расположена не внутри, значит, обнаружена граница контура. Если же точка оказалась внутри контура, то она становится новой затравочной точкой и поиск продолжается рекурсивно. Подобные алгоритмы применимы только к растровым устройствам.

 ЗАПОЛНЕНИЕ МНОГОУГОЛЬНИКОВ.

 Многие замкнутые контуры являются простыми многоугольниками. Если контур состоит из кривых линий, то его можно аппроксимировать подходящим многоугольником или многоугольниками.

  Простейший метод заполнения многоугольника состоит в проверке на принадлежность внутренности многоугольника каждого пиксела в растре. Затраты можно уменьшить путем вычисления для многоугольника прямоугольной оболочки. Как показано на рисунке проверяются только внутренние точки этой оболочки.

 

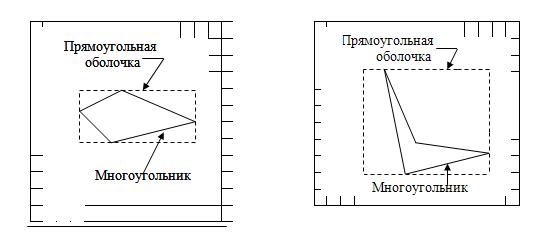
Использование прямоугольной оболочки для левого многоугольника намного сокращает число проверяемых пикселов, в то же время для правого многоугольника сокращение существенно меньше.

РАСТРОВАЯ РАЗВЕРТКА МНОГОУГОЛЬНИКОВ

Можно разработать более  эффективный метод, чем тест на принадлежность внутренней части, если воспользоваться тем фактом, что соседние пикселы, вероятно, имеют одинаковые характеристики (кроме граничных ребер). Это свойство называется пространственной когерентностью. Для растровых графических устройств соседние пикселы на сканирующей строке, вероятно, имеют одинаковые характеристики. Это когерентность растровых строк.

 Характеристики пикселов на данной строке изменяются только там, где ребро многоугольника пересекает строку. Эти пересечения делят сканирующую строку на области.

 

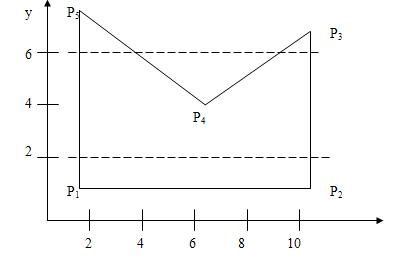
Для простого многоугольника на рисунке строка 2 пересекает  многоугольник при х=1 и х=11. Получаем три области:

  x < 1

  1<=x<=11

  x > 11

строка 6 делится на 5 областей:

x < 1

1<=x<=4

4<x<9

9<=x<=11

x>11

Совсем не обязательно, чтобы точки пересечения для строки 6 сразу определялись в фиксированном порядке (слева направо). Например, если многоугольник задается списком вершин Р₁Р₂Р₃Р₄Р₅а список ребер парами вершин Р₁Р₂, Р₂Р₃, Р₃Р₄, Р₄Р₅,Р₅Р₁, то для строки 6 будут найдены следующие точки пересечения с ребрами многоугольника 11, 9, 4, 1. Эти точки надо отсортировать в возрастающем порядке по х, т.е. получить 1, 4, 9, 11.

Для определения интенсивности, цвета и оттенка пикселов на сканирующей строке рассматриваются пары отсортированных точек пересечений. Для каждого интервала, задаваемого парой пересечений, используется интенсивность или цвет заполняемого многоугольника. Для интервалов между парами пересечений и крайних (от начала  строки до первой точки пересечения и от последней точки пересечения до конца строки) используется фоновая интенсивность или цвет. На нашем рисунке для строки 6 в фоновый цвет  установлены пикселы от 0 до 1, от 4 до 9 и от 11 до 12, тогда как пикселы от 1 до 4 и от 9 до 11 окрашены в цвет многоугольника.

Точное определение тех пикселов, которые должны активироваться, требуют некоторой осторожности. Рассмотрим простой прямоугольник, изображенный на следующем рисунке.

 
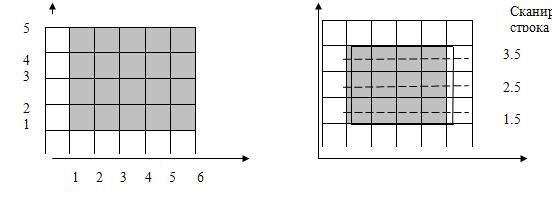
Прямоугольник имеет координаты (1,1), (5,1), (5,4), (1,4). Сканирующие строки с 1 по 4 имеют пересечения с ребрами многоугольника при х=1 и 5. Если пикселы адресуются координатами своего левого нижнего угла, значит, для каждой из этих сканирующих строк будут активированы пикселы с х-координанами 1, 2, 3, 4 и 5. На рисунке слева показан результат. Заметим, что площадь, покрываемая активированными пикселами, равна 20, в то время как настоящая площадь прямоугольника 12. 

Модификация системы координат сканирующей строки и теста активации устраняет эту проблему, как показано на рисунке справа. Считается, что сканирующие строки проходят через центр строк пикселов, т.е. через середину интервала. Тест активации модифицируется следующим образом: проверяется, лежит ли внутри интервала центр пиксела, расположенного справа от пересечения. Однако пикселы все еще адресуются координатами левого нижнего угла. Как показано на рисунке справа, результат данного метода корректен.

   Горизонтальные ребра не могут пересекать сканирующую строку и, таким образом, игнорируются. Это совсем не означает, что их нет на рисунке. Эти ребра формируются верхней и нижней строками пикселов, как показано на рисунке выше. Этот же рисунок иллюстрирует корректность верхнего и нижнего ребер многоугольника, полученных в результате модификации системы координат  сканирующих строк.

Дополнительная трудность возникает при пересечении сканирующей строки и многоугольника точно по вершине, как это показано на рисунке ниже.

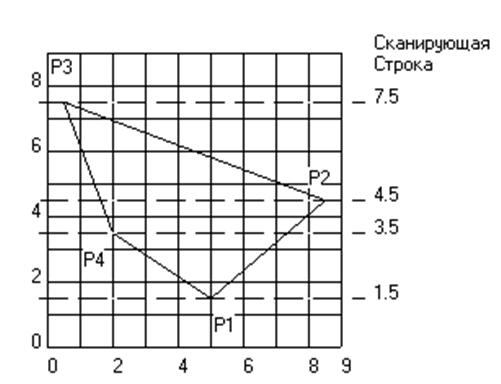
Правильный результат можно получить, учитывая точку пересечения в вершине два раза, если она является точкой локального минимума или максимума и учитывая ее один раз в противном случае. Определить локальный максимум или минимум многоугольника в рассматриваемой вершине можно с помощью проверки концевых точек двух ребер, соединенных в вершине. Если у обоих концов координаты больше, чем у вершины, значит, вершина является точкой локального минимума. Если  меньше, значит, вершина – точка локального максимума. Если одна больше, а другая меньше, следовательно, вершина не является ни точкой локального минимума, ни точкой локального максимума. На рисунке точка Р₁ – локальный минимум, Р₃ – локальный максимум, а Р₂, Р₄ – ни то, ни другое. Следовательно, в точках Р₁ и Р₃ учитываются два пересечения со сканирующими строками, а в Р₂ и Р₄ – одно.  

Алгоритмы заполнения с затравкой.

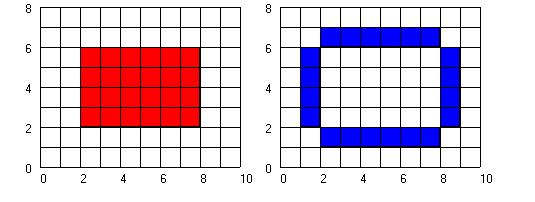
В этих алгоритмах предполагается, что известен хотя бы один пиксел из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пикселы, принадлежащие внутренней области. Области могут быть либо внутренне- либо гранично-определенными. Если область относится к внутренне-определенной, то все пикселы, принадлежащие внутренней части имеют один и тот же цвет или интенсивность, а все пикселы, внешние по отношению к области, имеют  другой цвет. Это продемонстрировано на рисунке слева. Если область относится к гранично-определенным, то все пикселы на границе области  имеют выделенное значение  или цвет, как показано на рисунке справа. Ни один из пикселов из внутренней части такой области не может иметь это выделенное значение. Алгоритмы, заполняющие внутренне-определенные области, называются внутренне-заполняющими, а алгоритмы для гранично-определенных областей гранично-заполняющими. Мы будем обсуждать гранично-заполняющие алгоритмы.

Внутренне- или гранично-определенные области могут быть 4- или 8-связными. Если область 4-связная, то любого пиксела в области можно достичь с помощью комбинации движений только в 4 направлениях: налево, направо, вверх, вниз. Для 8-связной области пиксела можно достичь с помощью комбинации движений в двух горизонтальных, двух вертикальных и четырех диагональных направлениях. Алгоритм заполнения 8-связной области заполнит и 4-связную область, однако обратное не верно. На следующем рисунке показаны простые примеры 4- и 8-связных внутренне-определенных областей.

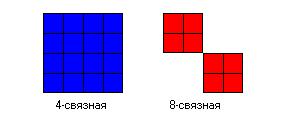
Хотя каждая из подобластей 8-связной области на рисунке слева является 4-связной, для перехода из одной подобласти в другую требуется 8-связный алгоритм. Однако, когда надо заполнить две отдельные 4-связные подобласти разными цветами, использование 8-связного алгоритма вызовет неправильное заполнение обеих подобластей одним и тем же цветом.

Простой алгоритм заполнения с затравкой.

Используя стек можно разработать простой алгоритм заполнения гранично-определенной области, который можно представить в следующем виде.

    Поместить затравочный пиксел в стек.

    Пока стек не пуст:

             Извлечь пиксел из стека

             Присвоить пикселу требуемое значение

             Для каждого из соседних к текущему 4-связных пикселов проверить: является ли    

             он граничным пикселом или не присвоено ли уже пикселу требуемое значение.

             Проигнорировать пиксел в любом из этих двух случаев. В противном случае

             поместить пиксел в стек.

Алгоритм можно модифицировать для 8-связных областей, если просматривать 8-связные пикселы, а не только 4-связные. Приведем более формальное изложение алгоритма, в котором предполагается существование затравочного пиксела и гранично-определенной области.

Простой алгоритм заполнения

Затравка (х,у) выдает затравочный пиксел

Push – процедура, которая помещает пиксел в стек

Рор – процедура, которая извлекает пиксел из стека

 Пиксел(х,у) = Затравка (х,у)

инициализируем стек

Push Пиксел(х,у)

While (стек не пуст)

    извлекаем пиксел из стека

Рор Пиксел(х,у)

If Пиксел(х,у) < >  Нов_значение then

    Пиксел(х,у) = Нов_значение

end if

проверим, надо ли помещать соседние пикселы в стек

If Пиксел(х + 1,у) < >  Нов_значение and

    Пиксел(х + 1,у) < >  Гран_значение then

    Push Пиксел(х + 1,у)

If Пиксел(х ,у + 1) < >  Нов_значение and

    Пиксел(х ,у + 1) < >  Гран_значение then

    Push Пиксел(х ,у + 1)

If Пиксел(х - 1,у) < >  Нов_значение and

    Пиксел(х - 1,у) < >  Гран_значение then

    Push Пиксел(х - 1,у)

If Пиксел(х ,у - 1) < >  Нов_значение and

    Пиксел(х ,у - 1) < >  Гран_значение then

    Push Пиксел(х,у - 1)

end if

end while

В алгоритме проверяются и помещаются в стек 4-связные пикселы, начиная с правого от текущего пиксела. Направление обхода против часовой стрелки

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.