Аналитическая модель информационной системы на основе марковских цепей

Для описания поведения системы в виде Марковской модели следует определить понятие состояния системы; выявить все состояния, в которых может находиться система; указать, в каком состоянии находится система в начальный момент; построить граф состояний, т.е. изобразить все состояния, например, кружками и возможные переходы из состояния в состояние – стрелками, соединяющими состояния (на рис. 3.1. выделено пять состояний); разметить граф, т.е. для каждого перехода указать интенсивность 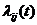 потока событий, переводящих систему из состояния  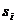в состояние :

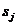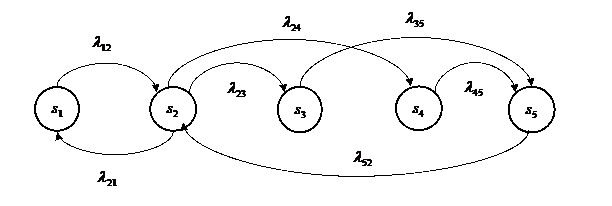
Рис. Пример графа состояний

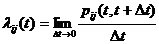                                                                              (3.7)
где 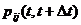 - вероятность перехода из состояния  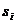в состояние  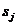за время от  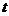до .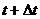
Для стационарных Марковских процессов интенсивности переходов не зависят от времени: 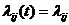, тогда .
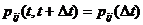Понятие состояния зависит от целей моделирования. В одном случае, например, оно может быть определено по состояниям элементов, каждый из которых может быть «свободен» или «занят»; в другом случае состояние системы определяется числом заявок, находящихся на обслуживании и в очередях.

В классе марковских процессов выделяют процессы с дискретными состояниями, называемые марковскими цепями. Когда множество состояний процесса 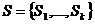 конечно, марковскую цепь называют конечной. Конечная марковская цепь может быть определена в непрерывном или дискретном времени. В первом случае переходы процесса из одного состояния в другое связываются с произвольными моментами времени  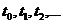и цепь называют непрерывной; во втором – только в фиксированные моменты времени, обозначаемые порядковыми номерами  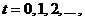и цепь называется дискретной.

Дискретная марковская цепь определяется:

1. множеством состояний ;
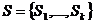2. матрицей вероятностей переходов 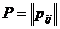,  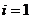   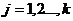 ,   , элементы которой характеризуют вероятности перехода процесса из состояния  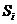в состояние ;
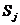3. вектором начальных вероятностей 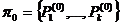, определяющим вероятности  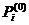того, что в начальный момент времени  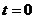процесс находится в состоянии .

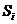Марковская цепь может быть представлена графом, вершины которого соответствуют состояниям цепи, а дуги ненулевым вероятностям переходов. На рис. 3.2 (а) представлен граф марковской цепи, имеющей 5 состояний и вектор начальных вероятностей 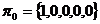. Вероятности переходов показаны на дугах графа.

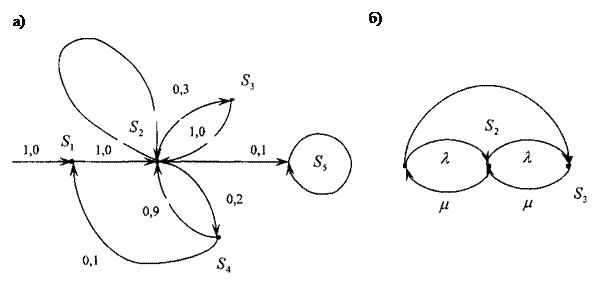
Рис. 3.2. Графы марковских цепей: а – дискретная, б – непрерывная

Марковская цепь порождает множество реализаций случайного процесса 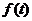, который представляется последовательностью состояний  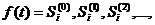соответствующих моментам времени 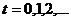. В зависимости от возможности перехода из одних состояний в другие марковские цепи делятся на поглощающие и эргодические цепи.
Поглощающая марковская цепь содержит поглощающее состояние, достигнув которого, процесс прекращается. Признаком поглощающей цепи является наличие в матрице 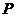 диагонального элемента 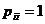. Так, марковская цепь, представленная на рис. 3.2, является поглощающей, так как содержит поглощающее состояние 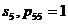. Для поглощающей цепи любой процесс в результате  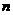шагов при  с вероятностью 1 попадает в поглощающее состояние.

Поглощающие марковские цепи широко используются в качестве временных моделей программ и вычислительных процессов. При моделировании программы состояния цепи отождествляются с модулями (операторами) программ, а матрица переходных вероятностей определяет порядок переходов между модулями, зависящий от структуры программы и исходных данных, значения которых определяют развитие вычислительного процесса. На такой модели можно вычислить число обращений к модулям программы и время выполнения программы, оцениваемой средними значениями, дисперсиями и при необходимости – распределениями. Аналогично вычислительный процесс, сводящийся к последовательности обращений к ресурсам системы в порядке, определяемом программой, можно представить поглощающей марковской цепью, состояния которой соответствуют использованию ресурсов системы – процессора и периферийных устройств, а переходные вероятности отображают порядок обращения к различным ресурсам.

Эргодическая марковская цепь представляет собой множество состояний, связанных матрицей переходных вероятностей таким образом, что из какого бы состояния процесс ни исходил, после некоторого числа шагов он может оказаться в любом состоянии. По этой причине состояния эргодической цепи называются эргодическими (возвратными). Процесс, порождаемый эргодической цепью, начавшись в некотором состоянии, никогда не завершается, а последовательно переходит из одного состояния в другое, попадая в различные состояния в разной частотой, зависящей от переходных вероятностей. Поэтому основная характеристика эргодической цепи – вероятности пребывания процесса в состояниях 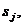 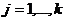 , или относительные частоты попадания процесса в состояния  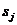и доля времени, которую процесс проводит в каждом из состояний. В качестве дополнительных характеристик эргодических цепей используются математическое ожидание и дисперсия времени (числа шагов) первого попадания в состояние  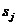из состояния  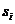и предельная корреляция числа попаданий в состояния  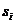и 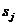.Эти характеристики определяются методами алгебраической теории марковских цепей.

Эргодические цепи широко используются в качестве моделей надежности систем. В этом случае состояния цепи соответствуют состояниям системы различающихся составом исправного и отказавшего оборудования. Переходы между состояниями связаны с отказами и восстановлением устройств и реконфигурацией связей между ними, выполняемой для сохранения работоспособности системы. Оценки характеристик эргодической цепи дают представление о надежности поведения системы в целом. Кроме того, эргодические цепи широко используются в качестве базовых моделей взаимодействия устройств с задачами, поступающими на обработку.

Непрерывная марковская цепь, поведение которой в любой момент времени подчиняется одному и тому же закону, называется однородной. Такая цепь задается матрицей интенсивностей переходов 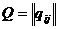, 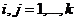. Интенсивность переходов определяется следующим образом:
,         ,
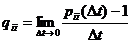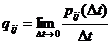где 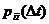 - вероятность перехода из состояния  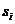в состояние  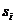за время .
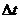Это означает, что если процесс находится в состоянии 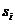, то вероятность перехода в течение промежутка времени 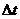в состояние 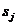, отличное от  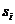равно 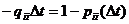. Аналогично вероятность перехода процесса из состояния  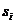в состояние  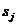равно .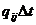
Интенсивность переходов должна удовлетворять условию
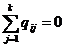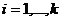,                                                                        (1)
На рис. 3.2 (б) представлен граф непрерывной Марковской цепи с тремя состояниями и дугами, нагруженными интенсивностями переходов. Матрица 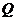 для данного графа, составленная с учетом условия (1) имеет вид:

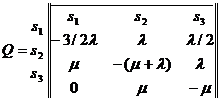
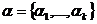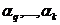Основной характеристикой непрерывной Марковской цепи является стационарное (финальное) распределение вероятностей состояний , где  - вероятности пребывания процесса в состояниях  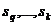соответственно. Значение вероятностей  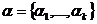определяется решением системы уравнений:
,     
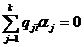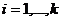
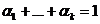                                                                                 (2)
Систему уравнений (2) называют уравнениями равновесия. Они составляются по графу Марковской цепи с учетом того, что в каждом состоянии входящий поток должен равняться исходящему потоку. 
Например, для цепи на рис. 3.2 (б) имеем:

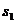
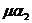
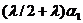
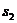
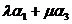
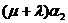
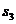
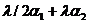
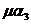
Система уравнений равновесия получается из условия равенства интенсивности входящего и исходящего потока
;
;
.
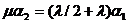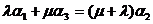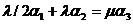В соответствии с Марковским свойством вся предыстория процесса сказывается на его поведении в будущем только через текущее состояние, которое и определяет дальнейший ход процесса. Таким образом, нет необходимости знать, как долго процесс находится в текущем состоянии. Отсюда следует, что распределение остающегося времени пребывания процесса в состоянии 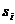 должно зависеть только от самого состояния, а не от времени пребывания в нем. Этим свойством обладает только одно распределение – экспоненциальное, функция плотности вероятности которого имеет следующий вид: 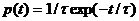, где 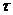 - параметр распределения, определяющий математическое ожидание случайной величины 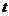. Таким образом, непременное свойство непрерывного Марковского процесса – экспоненциальность распределения времени пребывания в каждом из состояний.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.