Энтропия источника дискретных сообщений. Энтропия источников независимых и зависимых сообщений.

Во многих случаях, когда требуется согласовать канал с источником сообщений возникает потребность в характеристиках, которые позволяли бы оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся па одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и определяется выражением:  J(a) = - log P(a) = log m.При этом среднее количество информации равно log m. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле m.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ- редко. Поэтому знание числа сообщений m в ансамбле является недостаточным, необходимо иметь сведения о вероятности каждого сообщения: Р(а₁), Р(а₂ ), …, P(a_m).

Так как вероятности сообщений неодинаковы, то они несут различное количество информации: J(а_i)=- log P(а₁) Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(а_i ).

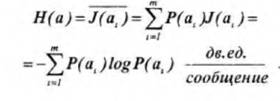  (1

Величина Н(а) называется энтропией. Энтропия Н(а) характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений a₁ и а₂ с вероятностями Р(а₁)= р и Р(a₂ ) =1- р. На основании (1) энтропия такого источника будет равна:

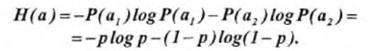
Зависимость Н(а) от р показана на рис.:

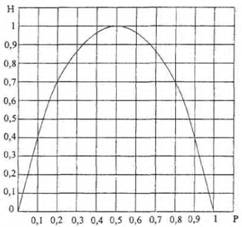
Максимум энтропии имеет место при р=1/2, т. е. когда ситуация является наиболее неопределенной. При р= 1 или р= 0, что соответствует передаче одного из сообщений а₁, или а₂, неопределенности отсутствуют. В этих случаях энтропия Н(а) равна нулю.

Среднее количество информации, содержащееся в пос­ледовательности из n-сообщений, равно: J_n = n* H(a).

Количество передаваемой информации можно увеличить не только за счет числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.

свойства энтропии источника независимых сообщений:

• энтропия - величина всегда положительная, так как 0 < Р(а_i) <=1;

• при равновероятных сообщениях, когда: Р(а₁ )= Р(а₂ )= ... = Р(а_m ) = Р(а) = 1/m , энтропия максимальна и равна:

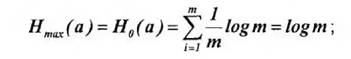
• энтропия равняется нулю лишь в том случае, когда все вероятности Р(a_t ) равны нулю, за исключением одной, величина которой равна единице;

• энтропия нескольких независимых источников равна сумме энтропии этих источников:

H(a,b,...,r) = Н(а)+Н(b) +... + Н(r).

Энтропия зависимых источников.

В реальных условиях имеют место статистические связи между сообщениями. Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью P(a_k,a_L) или условной вероятностью Р(a_L/а_k) , которая выражает вероятность появления сообщения a_L при условии, что известно предыдущее сообщение а_К.Количество информации, содержащейся в сообщении при условии, что известно предыдущее сообщение а_К будет равно: J(a_L/а_k) = - log P (a_L /а_k)

Среднее количество информации при этом определяется условной энтропией H(a_L /a_k), которая вычисляется как математическое ожидание информации J(a_L / a_k ) по всем возможным сообщениям а_к и a_L.

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимого сообщений можно записать неравенства:

H₀ (a) >= H₁(a) >= H₂ (a) >=…> = H_n(a)

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящейся в среднем на одно сообщение.