Критерии надежности невосстанавливаемых систем.Вероятность безотказной работы. Плотность распределения временибезотказной работы. Интенсивность отказов. Среднее время безотказнойработы.

Для невосстанавливаемых систем, чаще всего, используются четыре показателя надежности: вероятность безотказной работыP(t), плотность вероятности отказов (частота отказов) f(t), интенсивность отказов λ(t), среднее время безотказной работы (средняя наработка на отказ) T₀.

Вероятность безотказной работы P(t) есть вероятность того, что время работы системы до отказа окажется больше заданного времени t.

Р(t) – вероятность безотказной работы в течение времени t – вероятность того, что технический объект не откажет в течении времени t или что время ξ- время работы до отказа больше времени его функционирования, т.е.

Р(t)=Р(ξ >t)

0≤P(t) ≤1,  P(0)=1, P(+∞)=0

Определяется статистической оценкой

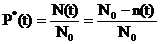
где N₀ – общее кол-во образцов

N(t) – число исправно работающих образцов

n(t) – число отказавших образцов за t.

Иногда пользуются понятием вероятности отказов  Q(t)=1-P(t)

Если P(t) – надежность системы, то Q(t) – ненадежность системы.

Плотность вероятности, или частота отказов, является дифференциальной функцией распределения.

f(t)=dQ(t)/dt= - dP(t)/dt   то же самое: f(t)=Q’(t)/dt= - P’(t)/dt

Статистически f(t) определяется отношение числа отказавших образцов в единицу времени к числу испытуемых образцов 

Интенсивность отказа λ(t) – это отношение плотности вероятности к вероятности безотказной работы

Среднее время безотказной работы системы – это математическое ожидание времени работы системы до отказа:

По статистическим данным:, где t_i- время б/о работы i-го образца

Пределы несобственного интеграла изменяются от 0 до ∞, так как время не может быть отрицательным.

Показатели надежности функционально связаны между собой: зная одну из функций P(t), Q(t), f(t), λ(t), можно определить три остальные.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.