Математические методы моделирования процессов и систем.

Математическое моделирование – это построение и использование математических моделей для исследования поведения систем (объектов) в различных условиях, для получения (расчета) тех или иных характеристик оригинала без проведения измерений или с небольшим их количеством. В рамках математического моделирования сложились два основных подхода:

-          аналитический;

-          имитационный.

-          Комбинированный.

Аналитический подход основывается на построении формульных зависимостей, связывающих параметры и элементы системы. Такой подход долгое время и был собственно математическим подходом. Однако при рассмотрении сложных систем строгие математические  зависимости весьма сложны, требуется большое количество измерений для получения требуемых значений параметров. Анализ характеристик процессов функционирования сложных систем с помощью только аналитических методов исследования наталкивается на значительные трудности, приводящие к необходимости существенного упрощения моделей либо на этапе их построения, либо в процессе работы с моделью, что снижает достоверность результатов.

Имитационный (статистический) подход в моделировании базируется на использовании предельной теоремы Чебышева при вероятностном представлении параметров системы. Теорема Чебышев: Если в N независимых испытаниях наблюдаются значения x₁ ..., X_n, случайной величины ξ, то при N->∞ среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию а, т. е. при любом ξ>0

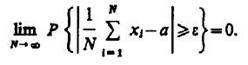
В рамках имитационного подхода используются аналитические зависимости между параметрами элементов системы, однако, эти зависимости имеют более обобщенный, упрощенный характер. Они значительно проще, нежели зависимости в рамках аналитического подхода. Множества случайных явлений (событий, величин) подчиняются определенным закономерностям, позволяющим не только прогнозировать их поведение, но и количественно оценить некоторые средние их характеристики, проявляющие определенную устойчивость. Принципиальное значение предельных теорем состоит в том, что они гарантируют высокое качество статистических оценок при весьма большом числе испытаний (реализаций) N.

Математическое моделирование систем, в том числе и информационных, имеет целью оптимизацию структуры систем, выбор наиболее оптимальных режимов функционирования систем, определение требуемых характеристик аппаратурного оборудования и программного обеспечения.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.