Передача информации происходит во времени, поэтому можно ввести понятие скорости передачи как количество информации, передаваемой в среднем за единицу времени. Для эргодических последовательностей сообщений, где допускается усреднение во времени, скорость передачи равна:
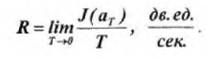 (1)
(1)
Здесь J(aT) - количество информации, содержащейся в последовательности сообщений aT, общая длительность которых равна Т, причем предполагается, что все сообщения, входящие в последовательность, имеют определенную длительность.
Количество информации, создаваемое источником сообщений в среднем за единицу времени, называется производительностью источника RH. Эту величину удобно выразить через энтропию источника Н(а). Действительно, приТ→ 0 можно считать J(аT) =n • Н(а) и Т=n• τ~, где n- число сообщений, а τ~- средняя длительность одного сообщения. Тогда, подставляя в (1) значения ,J (аT) ) и Т, получим:
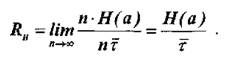 (2)
(2)
Если длительность всех сообщений одинакова и равна τ i , выражение (2) принимает вид:
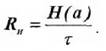 (3)
(3)
Отсюда следует, что наибольшей производительностью обладает источник с максимальной энтропией Н(а)max=logm :
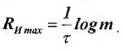 (4)
(4)
Выданная источником информация в виде отдельных сообщений поступает в канал связи, где осуществляются кодирование и ряд других преобразований, в результате которых информация переносится уже сигналами u, имеющими другую природу и в общем случае обладающими другими статистическими характеристиками.
Для сигналов также может быть найдена скорость передачи по каналу связи:
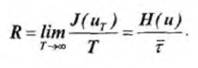 (5)
(5)
Высокая скорость передачи является одним из основных требований, предъявляемых к системам передачи информации. Однако в реальных условиях существует ряд причин, ведущих к ее ограничению. В реальном канале число используемых сигналов всегда конечно, поэтому энтропия в соответствии есть величина ограниченная:H(u)<=log m. (6)
С другой стороны, уменьшение длительности сигналов приводит, как известно, к расширению спектра, что ограничивается полосой пропускания капала. Это в конечном счете ставит предел уменьшению и средней длительности τ. Таким образом, существуют, по крайней мере, две причины: конечное число сигналов и конечная
длительность сигналов, которые не позволяют беспредельно повышать скорость передачи информации по каналу связи.
Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется пропускной способностью канала:
С = max R = max ( H(u)/τ~) дв.ед./ сек. (7)
Пропускная способность канала характеризует его предельные возможности в отношении передачи среднего количества информации за единицу времени. Максимум скорости R в выражении (7) ищется по всем возможным ансамблям сигналов и .
При передаче информации простейшими двоичными сигналами – телеграфными посылками - необходимая полоса пропускания канала зависит от частоты манипуляции Fm =1/2τ , которая по определению равна частоте первой гармоники спектра сигнала, представляющего собой периодическую последовательность посылок и пауз. Очевидно, минимальная полоса пропускания канала, при которой еще возможна передача сигналов, F= Fm. Отсюда максимальная скорость передачи двоичных сигналов по каналу без помех равна: C = V = 2Fm (Предел Найквиста) Понятие пропускной способности применимо не только ко всему каналу в целом, но и к отдельным его звеньям. Существенным здесь является то, что пропускная способность С' какого-нибудь звена не превышает пропускной способности С’’второго звена, если оно расположено внутри первого. Соотношение С'<= С’’ обусловлено возможностью дополнительных ограничений, накладываемых на участок канала при его расширении и снижающих пропускную способность.