Правила «если-то» для представления знаний.

Правила «если-то» для представления знаний

В качестве кандидата на использование в экспертной системе можно рассматривать, в принципе, любой непротиворечивый формализм, в рамках которого можно описывать знания о некоторой проблемной области. Однако самым популярным формальным языком представления знаний является язык правил типа если-то, называемых также продукциями. Вот примеры:

· если предварительное условие Р то заключение (вывод) С

· если ситуация S то действие А

· если выполнены условия С1 и С2 то не выполнено условие С

Если-то-правила обычно оказываются весьма естественным выразительным средством представления знаний. Кроме того, они обладают следующими привлекательными свойствами:

· Модульность: каждое правило описывает небольшой, относительно независимый фрагмент знаний.

· Возможность инкрементного наращивания: добавление новых правил в базу знаний происходит относительно независимо от других правил.

· Удобство модификации (как следствие модульности): старые правила можно изменять и заменять на новые относительно независимо от других правил.

· Применение правил способствует прозрачности системы.

Последнее свойство - это важное, отличительное свойство экспертных систем. Под прозрачностью мы понимаем способность системы к объяснению принятых решений и полученных результатов. Применение если-то-правил облегчает получение ответов на следующие основные типы вопросов пользователя:

(1) Вопросы типа как: Как вы пришли к этому выводу?

(2) Вопросы типа почему: Почему вас интересует эта информация?

Если

1 тип инфекции - это первичная бактериемия и

2 материал для посева был отобран стерильно, и

3 предполагаемые ворота инфекции - желудочно- кишечный тракт

То

имеются веские аргументы (0.7) за то,

что инфекционный агент является бактерией

Рис. 14. 2. Если-то-правило медицинской консультативной системы MYCIN (Shortliffe, 1976). Параметр 0.7 показывает степень доверия этому правилу.

Если-то-правила часто применяют для определения логических отношений между понятиями предметной области. Про чисто логические отношения можно сказать, что они принадлежат к категорическим знаниям, категорическим - потому, что соответствующие утверждения всегда, абсолютно верны. Однако в некоторых предметных областях, таких, как медицинская диагностика, преобладают мягкие или вероятностные знания. Эти знания являются мягкими; в том смысле, что говорить об их применимости к любым практическим ситуациям можно только до некоторой степени (часто, но не всегда). В таких случаях используют модифицированные если-то-правила, дополняя их логическую интерпретацию вероятностной оценкой. Например:

если условие А то заключение В с уверенностью F

Правила, содержащиеся в базе знаний, имеют вид

ИмяПравила : если Условие то Заключение

где Заключение - это простое утверждение, а Условие - это набор простых утверждений, соединенных между собой операторами и и или. Мы также разрешим в части условия использовать оператор не, хотя и с некоторыми оговорками. Заметим, что оператор и связывает операнды сильнее, чем или, что соответствует обычным соглашениям.

Рассмотрим еще одну небольшую базу знаний, которая может помочь локализовать неисправности в простой электрической схеме, состоящей из электрических приборов и предохранителей. Электрическая схема показана на рис. 14.6. Вот одно из возможных правил:

Если

лампа1 включена и

лампа1 не работает и

предохранитель1 заведомо цел

то

лампа1 заведомо неисправна.

Вот другой пример правила:

Если

радиатор работает

то

предохранитель1 заведомо цел.

Эти два правила опираются на некоторые факты (относящиеся к нашей конкретной схеме), а именно что лампа1 соединена с предохранитель1 и что лампа1 и радиатор имеют общий предохранитель. Для другой схемы нам понадобится еще один набор правил. Поэтому было бы лучше сформулировать правила в более общем виде (используя прологовские переменные) так, чтобы они были применимы к любой схеме, а затем уже дополнять их информацией о конкретной схеме. Например, вот одно из полезных правил: если прибор включен, но не работает, а соответствующий предохранитель цел, то прибор неисправен.

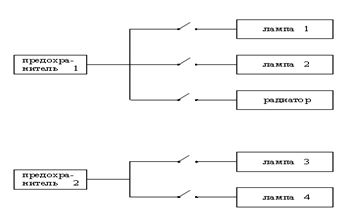
Рис. 14. 6. Соединения между предохранителями и приборами в простой электрической схеме.

На наш формальный язык это транслируется так:

правило_поломки:

если

Прибор включен и

не (Прибор работает) и

Прибор соединен с Предохранитель и

Предохранитель заведомо цел

То

Прибор заведомо неисправен.

База знаний такого рода показана на рис. 

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.