Канонические графы. Правила построения. Унаследованные свойства.

В концептуальном графе есть узлы-концепты и узлы-связи (связывающие узлы). Каждая входящая в связывающий узел стрелка (или выходящая из него) соединена с узлом концептом. Однако некоторые комбинации узлов бессмысленны. Например, можно изобразить графом фразу «удалить последнее слово следующей строки» (какого-то текста). С позиций грамматики эта фраза синтаксически и семантически корректна. Напротив фраза «удалить последнюю строку следующего слова» синтаксически корректна, но абсурдна (семантически некорректна). Чтобы исключить графы нереальных (невозможных) ситуаций области рассуждений, Сова определил канонические (семантически корректные) графы разрешённых комбинаций слов. Каждый составляет представление о мире, выразимом каноническими графами, исходя из личного опыта.

Таким образом, возможный путь построения таких графов следующий: мозг вырабатывает систему концептов, базируясь на поступающих ощущениях, и так расставляет сформированные концепты, чтобы они отражали реальную ситуацию. Следовательно, можно считать, что мозг строит канонические графы, представляющие, вообще говоря, очевидности (другими словами тавтологии исчисления предикатов). Новые канонические графы строятся из имеющихся по определённым правилам построения. Эти правила формируют порождающую грамматику для концептуальных графов точно так же, как это делается посредством правил переписывания Хомского в случае порождающих грамматик для синтаксических структур естественных языков.

Правила построения

Сова предложил четыре правила построения для конструирования нового канонического графа g из имеющихся графов g1 и g2 (которые могут совпадать):

Правило конъюнкции: Если узел-концепт с1 в g1 идентичен узлу-концепту с2 в g2, то g получается удалением с2 и соединением с с1 всех связывающих узлов, которые были связаны с с2 в g2.

Правило упрощения. Если концептуальный граф g содержит два идентичных (соединенных с одними и теми же узлами-концептами) связывающих узла, то можно удалить один из них вместе со связанными с ним стрелками.

Правило копирования: граф g есть копия графа g1.

Правило ограничения: Для любого концепта с концептуального графа g тип (с) можно заменить неким подтипом. Если с – концепт совокупности, то её ссылку можно заменить индивидуальным указателем (какой-то конкретизацией). Такие замены разрешены лишь тогда, когда ссылка для с соответствует типу (с).

Проиллюстрируем эти правила на концептуальных графах представленных на следующем рисунке. Граф без элементов с (2) – для фразы «Жак срочно посылает книгу кому-то» Граф без элементов с (1) – для фразы «Жак посылает почтой книгу Мари». Применение правила конъюнкции к этим двум графам даёт весь граф изображённый на рисунке. Можно было бы далее применить к последнему графу правило ограничения, заменяя обозначенную х совокупность «кому-то» меньше совокупностью «женщина». Однако прежде надо убедиться в свойстве «Мари – женщина». Предыдущие правила являются фактически правилами суждения: ограничение сужает концепты, а конъюнкция добавляет условия на графах. Аналогично можно определить правила расширения, которые представляют собой правила, обратные к правилам суждения.

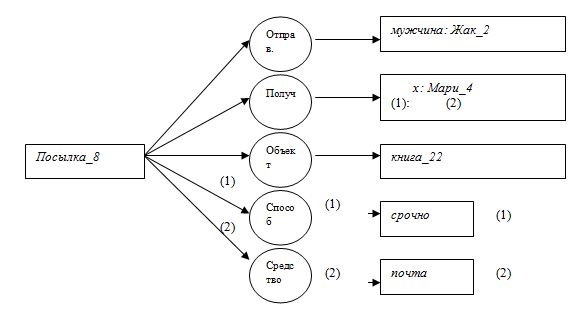
Унаследованные свойства

Форма различных концептов, типов и множеств во многих приложениях иерархическая. Классификация животных по родам, видам, семействам, отрядам и т.д. – классический пример иерархии. Другой пример – множество слов в словаре. Книги, транспортные средства и постройки образуют иерархически упорядоченные множества. Можно иерархически классифицировать и абстрактные концепты действий, состояний, свойств, убеждений. Используемые в обыденных рассуждениях классификации, как правило, сложнее биологических: индивид принадлежит, вообще говоря, не одному типу и не одному множеству. Однако в большинстве случаев для ИИ используются сравнительно простые иерархии.

Сначала проиллюстрируем иерархию типов на примере, а затем дадим формальное определение. Если известно, что Жак (представленный конкретизацией Жак_2) – профессор университета, то можно сделать заключение о наличии у него докторской степени и о том, что он работает в университете. Информация «Жак – профессор университета» предоставила нам целую цепочку сведений о Жаке. Унаследованными называют такие свойств, которые можно вывести подобным образом. Особых причин детально останавливаться на них нет. Ясно, что кое-какие характеристики профессоров университета можно описать исходя из принадлежности к профессуре; некоторые характеристики профессуры выносятся из того факта, что они содержатся в совокупности работников умственного труда, и, в конечном счёте, всех людей. Соображения эффективности побуждают нас не связывать с Жаком все общие профессоров университета, вообще профессоров и, наконец, всех людей. Весьма общее свойство, как например, «У Жака две руки и две ноги», сопоставляется узлу, характеризующему всех людей. Это даёт возможность не провозглашать наличие указанного свойства отдельно, для каждого индивида.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.