Рассуждения, использующие логические формулы.Рассуждения по поводу знаний.

Исчисление предикатов содержит правила вывода, применимые к одним логическим формулам для получения других. Особенно важны правила «modus ponens» ( Если Х и (Х Y) – теоремы, то Y есть теорема) и «обобщения» (Если х не связана в теореме Р, то хР – теорема). Правила вывода порождают некоторое множество формул из примитивных (исходных, первоначальных) формул. В исчислении предикатов выведенные формулы называются «теоремами», а последовательность примененных для их получения правил вывода (с указанием используемых в них формул) – «доказательством теоремы». Многочисленные приложения исчисления предикатов к ИИ можно толковать как методы доказательства теорем.

При доказательстве теорем обычно используют процедуры опровержения. Множество гипотез {Hj}, подходящих для доказательства теоремы, добавляют к множеству присущих области экспертизы аксиом {Ai}. Затем стремятся получить опровержение (или прийти к противоречию), присоединяя {¬С} – отрицание утверждения теоремы – к системе {Hj, Ai} и пытаясь доказать формулу

.

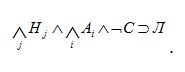
Эта формула логически эквивалентна формуле

.

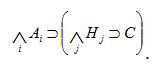
Процедуры, позволяющие строить доказательства формул такого типа, называются «доказательствами посредством опровержения». Они помогают избегать менее перспективных направлений поиска. Системы доказательства теорем во многих приложениях включают формулы логики предикатов с переменными, связанными кванторами существования. В таких случаях доказательства позволяют находить конкретизации этих переменных.

Например, интересно выяснить, можно ли формулу хС(х) логически вывести из гипотез и аксиом. Если да, то хотелось бы знать конкретизацию для х в терминах вывода. Попытка доказать хС(х) из {Hj, Ai} должна быть конструктивной. Проиллюстрируем подобное доказательство следующим примером.

Рассуждения по поводу знаний

В большинстве встречающихся в ИИ систем относящихся к области экспертизы знания делятся на две категории: «факты» и «правила» . Факты – это данные (представленные предикатами), касающиеся области экспертизы. Например, данные о персонале некоторого университета составляют множество фактов.

·                   Факт(1)

По-русски: Жак – профессор факультета информатики.

Логически: Проф(Инфо, Жак_2).

·                   Факт(2).

По-русски: Мари – студентка математического факультета,

Логически: Студ (Мат, Мари-4).

Правила – это данные, представленные с помощью импликации или в иной эквивалентной логической форме. Они представляют собой обобщающие знания об области экспертизы.

·                   Правило(1)

По-русски: Если y – профессор факультета х и w студент(ка) факультета z при x≠z, то y может служить внешним экзаменатором для w.

Логически: Проф (x,y)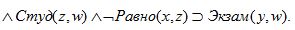

Задача доказательства (обоснования) теоремы состоит в установлении выводимости из фактов и правил некой формулы («предложения-цели», «заключения»), представляющий некоторый вопрос.

·                   Предложение-цель (1).

По-русски: Может ли Жак служить внешним экзаменатором для Мари?

Логически: Экзам(Жак_2. Мари_4).

Можно применять различные приемы для выработки стратегий доказательства теоремы.

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.